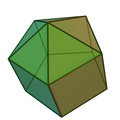
五角锥柱
在几何学中,五角锥柱是指底面为五边形的锥柱体,或是将底面全等的五角锥与五角柱叠合所形成的立体。若底面为正五边形则称为正五角锥柱。五角锥柱具有11个面、20个边、和11个顶点,每个五角锥柱皆为一个十一面体。
 | |||
| 类别 | 棱锥柱 约翰逊多面体 J8 - J9 - J10 | ||
|---|---|---|---|
| 对偶多面体 | 五角锥柱(自身对偶) | ||
| 识别 | |||
| 鲍尔斯缩写 | epeppy | ||
| 数学表示法 | |||
| 康威表示法 | P5+Y5 | ||
| 性质 | |||
| 面 | 11 | ||
| 边 | 20 | ||
| 顶点 | 11 | ||
| 欧拉特征数 | F=11, E=20, V=11 (χ=2) | ||
| 组成与布局 | |||
| 面的种类 | 三角形×5 正方形×5 五边形×1 | ||
| 顶点布局 | 5(42.5) 5(32.42) | ||
| 对称性 | |||
| 对称群 | C5v, [5], (*55) C5v群 | ||
| 旋转对称群 | C5, [5]+, (55) | ||
| 特性 | |||
| 凸、demi-regular | |||
| 图像 | |||
| |||
约翰逊多面体
编辑考虑一个正五角锥柱,若每一个面皆为正多边形,则为92种约翰逊多面体(J9)中的其中一个,也是锥柱体的一种,可由约翰逊多面体中的正五角锥与帕雷托立体中的半正五面体于相等大小的五边形面接合而组成。这92种约翰逊多面体最早在1966年由约翰逊·诺曼(Norman Johnson)命名并给予描述。
相关多面体
编辑| 二角锥柱 | 三角锥柱 | 四角锥柱 | 五角锥柱 | 六角锥柱 | 七角锥柱 | ... | 圆锥柱 |
|---|---|---|---|---|---|---|---|
参见
编辑| 这是一篇与多面体相关的小作品。您可以通过编辑或修订扩充其内容。 |