八面半八面体
在几何学中,八面半八面体是一种非凸多面体,属于星形多面体及均匀多面体[1],也可以归类在非凸均匀多面体,其索引为U3。八面半八面体由8个正三角形和4个正六边形组成,且每个顶点对应的角皆相等,因此也可以被归类为拟正多面体[2],然而由于这个立体同时具备半多面体的特性,因此被部分学者分成一类新的立体,即拟正半多面体(Versi-Regular Polyhedra),这类立体共有九个,最早在1881年由亚伯特·巴杜罗(Albert Badoureau)发现并描述[3]。特别地,这个立体的边长与外接球半径相等[4]。八面半八面体可以与星形八面体共同堆砌填满空间,因此曾应用于建筑结构中。[5]
 | |||||
| 类别 | 星形均匀多面体 | ||||
|---|---|---|---|---|---|
| 对偶多面体 | 八面半无穷星形八面体 | ||||
| 识别 | |||||
| 名称 | 八面半八面体 | ||||
| 参考索引 | U3, C37, W68 | ||||
| 鲍尔斯缩写 | oho | ||||
| 数学表示法 | |||||
| 考克斯特符号 | |||||
| 威佐夫符号 | 3/2 3 | 3 | ||||
| 性质 | |||||
| 面 | 12 | ||||
| 边 | 24 | ||||
| 顶点 | 12 | ||||
| 欧拉特征数 | F=12, E=24, V=12 (χ=0) | ||||
| 亏格 | -1 | ||||
| 组成与布局 | |||||
| 面的种类 | 8个三角形{3} 4个六边形{6} 存在半三角形{3/2} 一种抽象多胞形 | ||||
| 面的布局 | 8{3}+4{6} | ||||
| 顶点图 | 3.6.3/2.6 | ||||
| 对称性 | |||||
| 对称群 | Oh, [4,3], *432 | ||||
| 特性 | |||||
| 均匀 | |||||
| 图像 | |||||
| |||||
性质
编辑八面半八面体共有12个面、24条边和12个顶点[6][7],是一种十二面体,每个顶点都是2个正三角形和2个六边形的公共顶点。[6]
定向性
编辑八面半八面体是唯一可定向且欧拉示性数为零的半多面体,[8]这意味着其具有拓扑环面的性质。[9]
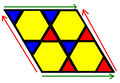
| 八面半八面体 |
八面半八面体在拓朴上的展开图可以排布为分割成8个正三角形和4个正六边形的菱形。所有顶点的角亏为零 |
这个展开图是截半六边形镶嵌的一部分,在威佐夫符号中计为3 3 | 3、考克斯特-狄肯记号计为 |
二面角
编辑八面半八面体仅有一种二面角,为三角形和六边形的棱之交角,其值为三分之一的反余弦值[10][11]:
其值约为70度31分43.6秒
顶点座标
编辑由于其凸包为截半立方体,因此其12顶点会与截半立方体相同,为(0, ±1, ±1),(±1, 0, ±1),(±1, ±1, 0),若边长为a,则座标要缩放 倍。[12]
作为简单多面体
编辑八面半八面体具有抽象多胞形半三角形面和互相相交的六边形面,但若去除相交的面作为一个简单多面体,则其可以视为由32个正三角形组成的凹多面体[13][14]。这种多面体共有32个面、48条边和13个顶点,其结构与四角化截半立方体拓朴同构,不过四角化截半立方体有18个顶点而这种多面体仅有13个顶点是因为有6个顶点在中心共用。另一方面,这个立体也可以视为由8个正四面体组合而成。[15]:103
-
四角化截半立方体
-
截半立方体
-
倒四角化截半立方体
八面半八面体
对偶多面体
编辑| 类别 | 无穷星形多面体 | |
|---|---|---|
| 对偶多面体 | 八面半八面体 | |
| 识别 | ||
| 名称 | 八面半无穷星形八面体 | |
| 参考索引 | DU3 | |
| 数学表示法 | ||
| 考克斯特符号 | ||
| 性质 | ||
| 面 | 12 | |
| 边 | 24 | |
| 顶点 | 12 | |
| 欧拉特征数 | F=12, E=24, V=12 (χ=0) | |
| 组成与布局 | ||
| 面的种类 | 12个四条棱的抽象多胞形 | |
| 顶点图 | 每个顶点周围都有3个面 | |
| 对称性 | ||
| 对称群 | Oh, [4,3], *432 | |
| 图像 | ||
| ||
八面半八面体的对偶多面体是八面半无穷星形八面体。其外观与立方半无穷星形八面体相同[16]。
从定义上来看,对偶多面体的面会与原始立体的顶点图相同,同时顶点周围之面的排列方式会和原始立体的面之边相同,也就是说对偶多面体的顶点图为原始立体的面[17]。由于八面半无穷星形八面体是八面半八面体的对偶多面体,而八面半八面体的12个顶点皆为4个面的公共顶点,因此八面半无穷星形八面体的面理应具有12个面,每个面由4个边组成[7]。然而八面半八面体有部分面几何中心落在整个立体的几何中心上,因此其对偶多面体的顶点会落在无穷远处,即无穷实射影平面上的点。[18]一般来说,这样的立体无法被具象化[7]。为了具像化这种立体,温尼尔在著作《对偶模型》中将其描述为由无限高的柱体组合构成的立体,在这样的视觉化方式下,八面半八面体外观为由4个无限高的六角柱构成的立体[18]。
相关多面体
编辑-
八面半八面体
八面半八面体可透过截去皮特里立方体的所有顶点来构造,也就是说,八面半八面体可以视为截半的皮特里立方体。[20][21]
-
八面半八面体
八面半八面体可以视为是截半立方体经过刻面后的结果[4],而立方半八面体也可以视为是刻面的截半立方体[22]。
| 截半立方体 | 立方半八面体 | 八面半八面体 | ||
|---|---|---|---|---|
| 八面体对称 | 四面体对称 | 八面体对称 | 四面体对称 | |
| 2 | 3 4 | 3 3 | 2 | 4/3 4 | 3 | 3/2 3 | 3 | |
中心八面半八面体数
编辑中心八面半八面体数是一种排列成八面半八面体的有形数。第n个中心八面半八面体数可以表示为 [23]。由于八面半八面体数与截半立方体共用相同的顶点排列方式,因此数列前两项与中心截半立方体数(OEIS数列A005902)相同,第三项开始少去了八面半八面体数相对于截半立方体缺少的6个四角锥[23]
前几个中心八面半八面体数为:
参见
编辑参考文献
编辑- ^ Wolfram, Stephen. "Octahemioctahedron". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- ^ George W. Hart. Quasi-Regular Polyhedra. 1996 [2021-09-05]. (原始内容存档于2021-08-30).
- ^ Jean Paul Albert Badoureau. Mémoire sur les Figures Isocèles. Journal de l'École polytechnique. 1881, (49): 47-172.
- ^ 4.0 4.1 Weisstein, Eric W. (编). Octahemioctahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Hisarligil, Hakan and Hisarligil, Beyhan Bolak. The Geometry of Cuboctahedra in Medieval Art in Anatolia. Nexus Network Journal (Springer). 2018, 20 (1): 125–152.
- ^ 6.0 6.1 Uniform Polyhedra 03: Octahemioctahedron. mathconsult. [2016-08-31]. (原始内容存档于2020-02-17).
- ^ 7.0 7.1 7.2 Vladimir Bulatov. octahemioctacron. Polyhedra Collection, bulatov.org. [2021-07-30]. (原始内容存档于2020-02-23).
- ^ The Octahemioctahedron. 西密歇根大学. [2016-08-31]. (原始内容存档于2016-03-14).
- ^ David A. Richter. The Octahemioctahedron. [2016-08-31]. (原始内容存档于2016-03-14).
- ^ Jean Paul Albert Badoureau, Mémoire sur les Figures Isocèles, Journal de l'École polytechnique 49 (1881), 47-172.
- ^ Versi-Regular Polyhedra: Octahemioctahedron. dmccooey.com. [2016-08-31]. (原始内容存档于2019-10-03).
- ^ Klitzing, Richard. octahemioctahedron, oho. bendwavy.org. [2021-09-06]. (原始内容存档于2021-01-23).
- ^ Gijs Korthals Altes. 作為簡單多面體的八面半八面體展開圖 (PDF). korthalsaltes.com. [2016-08-31]. (原始内容 (PDF)存档于2016-06-15).
- ^ Robert Webb. Octahemioctahedron. software3d.com. [2021-09-07]. (原始内容存档于2021-07-29).
- ^ Wenninger, M.J. Polyhedron Models. Cambridge University Press. 1974 [2021-09-06]. ISBN 9780521098595. LCCN 69010200. (原始内容存档于2021-08-31).
- ^ Weisstein, Eric W. (编). Octahemioctacron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Weisstein, Eric W. (编). Dual Polyhedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ 18.0 18.1 Wenninger, Magnus, Dual Models, Cambridge University Press, 2003 [1983], ISBN 978-0-521-54325-5, MR 0730208, doi:10.1017/CBO9780511569371 (Page 101, Duals of the (nine) hemipolyhedra)
- ^ HİSARLIGİL, Hakan and HİSARLIGİL, Beyhan BOLAK. The third dimension of the Magdouh Mosaic in Antioch. Journal of Mosaic Research. 2019, (12): 107-118},.
- ^ {6,3}(2,2), Petrie dual of the cube. Regular Map database - map details. [2021-07-30].
- ^ octahemioctahedron. Regular Map database - map details. [2021-07-30]. (原始内容存档于2021-07-25).
- ^ Weisstein, Eric W. (编). Cubohemioctahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ 23.0 23.1 Sloane, N.J.A. (编). Sequence A274974 (Centered octahemioctahedral numbers). The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.