十九面体

在几何学中，十九面体是指有19个面的多面体，在十九面体当中没有任何一个形状是正多面体，换言之即正十九面体并不存在，但仍有许多由正多边形组成的十九面体，例如正十七角柱，与之拓朴结构类似的十九面体曾被用于在形状稳定性的证明。

十九面体

部分的十九面体
扭棱半立方体	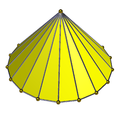十八角锥
十七角柱

常见的十九面体是十七角柱和十八角锥，也有一些化学结构是十九面体，例如有一种十二个顶点的分子构型，由其在几何上由十八个三角形和一个四边形组成。此外要构成十九面体至少要有12个顶点。

常见的十九面体

常见的十九面体包含了一些锥体、柱体和一些由锥体与柱体组合并包含19个面形状，亦有一些拓朴结构明显与锥体、柱体不同的十九面体，例如空间填充十三面体的对偶多面体。

十八角锥

十八角锥

十八角锥是一种底面为十八边形的锥体，是十九面体的一种，其具有19个面、36条边和19个顶点，其对偶多面体是自己本身。正十八角锥是一种底面为正十八边形的十八角锥，在施莱夫利符号中可以用{}∨{18}来表示。底边长为$s$、高为$h$的正十八角锥体积$V$和表面积$S$为：

$V={\frac {3hs^{2}\cot {\frac {\pi }{18}}}{2}}\approx 8.50692hs^{2}$

$S={\frac {9s\left({\sqrt {4h^{2}+s^{2}\cot ^{2}{\frac {\pi }{18}}}}+s\cot {\frac {\pi }{18}}\right)}{2}}\approx 4.5s\left({\sqrt {4h^{2}+32.1634s^{2}}}+5.67128s\right)$

十七角柱

十七角柱

十七角柱是一种底面为十七边形的柱体，是十九面体的一种，由19个面51条边和34个顶点组成。正十七角柱代表每个面都是正多边形的十七角柱，其每个顶点都是2个正方形和1个十七边形的公共顶点，顶点图以$4{.}4{.}17$表示，因此具有每个角等角的性质（点可递），可以归类为半正十九面体，不过他跟其他较接近球形的半正多面体相比之下变得比较扁一些。

正十七角柱在施莱夫利符号中可以用{17}×{}或t{2,17}来表示，在考克斯特符号中可以用来表示，在威佐夫符号中可以利用2 17 | 2来表示，在康威多面体表示法中可以利用P17来表示。底边长为$s$、高为$h$的正十七角柱体积$V$和表面积$S$为：

$V={\frac {17hs^{2}\cot {\frac {\pi }{17}}}{4}}\approx 22.7355hs^{2}$

$S=17s\left(h+{\frac {s\cot {\frac {\pi }{17}}}{2}}\right)\approx 17s\left(h+2.67476s\right)$

九角锥柱

九角锥柱是指底面为九边形的角锥柱，由19个面、32条边和19个顶点组成，是一种十九面体。其对偶多面体为九角锥台锥，由于拓朴结构与九角锥柱相同，因此有时会被视作自身对偶多面体。

九角锥台锥

九角锥台锥是指由九角锥台和九角锥组合成的多面体，其有两种形式：一种是九角锥叠在九角锥台较小的九边形面、另一种是九角锥叠在九角锥台较大的九边形面。后者可以视为只截去一个顶点的双九角锥。

九角锥台锥的拓朴结构与九角锥柱相同，因为九角锥柱可以借由缩放其九边形面使图形变形成九角锥台锥。

十七角锥台

十七角锥台一种底面为时七边形的锥台，可以视为切去一个顶点的十七角锥。通常其两个底面形状会有差异或者相似，而两个底面都全等的十七角锥台与十七角柱无异，因此十七角锥台的拓朴结构与十七角柱相同，因为十七角柱可以借由缩放其十七边形面使图形变形成十七角锥台。

六角锥反角柱

六角锥反角柱是指底面为六边形的角锥反角柱，可以视为一个六角锥与一个反六角柱底面对底面的组合。

六角锥反角柱不是一个詹森多面体，因为当其所有面都是正多边形时，其中六个正三角形将会共面，而导致图形退化成反六角柱。

相同的情形也出现在双六角锥反角柱上，必须要将部分正多边形面拉长或扭曲才能构成多面体，导致其无法以所有面皆为正多边形的形式存在，因此这些多面体可以被归类为拟詹森多面体。

对偶多面体为十九面体的多面体

有些多面体具有19个顶点，因此其对偶多面体为十九面体。例如空间填充十三面体具有19个顶点，因此其对偶多面体是一个十九面体。

空间填充十三面体的对偶多面体

空间填充十三面体的对偶多面体

空间填充十三面体的对偶多面体是一种19面体，其可以视为一种经过扭棱变换的结果，其对应的原像与半立方体类似，但又不相同，其对应的原像有面积为零的退化面。

这个多面体一共有19个面、30条边和13个顶点，其面由16个三角形和3个梯形所组成。其对偶多面体可以独立填满整个三维空间。

十九面体列表

名称	种类	图像	符号	顶点	边	面	χ	面的种类	对称性	展开图
十七角柱	棱柱体		t{2,17} {17}x{}	34	51	19	2	2个十七边形 17个矩形	D17h, [17,2], (*17 2 2), order 68
十八角锥	棱锥体		( )∨{18}	19	36	19	2	1个十八边形 18个三角形	C18v, [18], (*18 18)
九角锥柱	角锥柱		P9+Y9	19	36	19	2	9个三角形 9个正方形 1个九边形	C9v, [9], (*99)
九角锥台锥	截角双锥			19	36	19	2	1个九边形 9个梯形 9个三角形	C9v, [9], (*99)
十七角锥台	锥台			34	51	19	2	2个十七边形 17个梯形	D17h, [17,2], (*17 2 2), order 68
六角锥反角柱	角锥反角柱			13	30	19	2	1个六边形 18个三角形	C6v, [6], (*66)
六角化六角帐塔	帐塔锥			19	36	19	2	12个三角形 6个矩形 1个12边形	C6v, [6], (*66)
空间填充十三面体 的对偶多面体	扭棱半立方体			13	30	19	2	16个三角形 3个梯形
侧锥十四角柱			A14+Y4			19		4个正三角形 13个正方形 2个十四边形	C2v
二侧锥十一角柱			P11+2Y4			19		8个正三角形 9个正方形 2个十一边形	C2v

参见

• 十九边形：同为含19个维面（facet）的形状，但是位于二维空间。