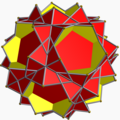
大五角化十二面体

在几何学中，大五角化十二面体（Great pentakis dodecahedron）是一种非凸等面多面体，由60个全等且互相相交的等腰三角形面组成，是均匀多面体——小星形截角十二面体的对偶多面体，可由大十二面体经向内五角化变换构成。由于其对偶多面体小星形截角十二面体有通过非常接近整体几何中心的面，因此导致其外观有非常锐利的尖角。整个立体共有12个这种尖角，若只考虑这些尖角，整个立体可以视为由正十二面体的每个面上加入锥高非常高的五角锥来构成这些尖角，因此这个立体也可以视为五角化十二面体的一种变体。

大五角化十二面体

类别	均匀多面体对偶 星形多面体
对偶多面体	小星形截角十二面体
识别
名称	大五角化十二面体
参考索引	DU58
数学表示法
考克斯特符号
性质
面	60
边	90
顶点	24
欧拉特征数	F=60, E=90, V=24 （χ=-6）
组成与布局
面的种类	60个锐角等腰三角形
对称性
对称群	Ih, [5,3], *532
特性
等面、非凸
图像
小星形截角十二面体 （对偶多面体）

性质

大五角化十二面体由60个面、90条边和24个顶点组成，是一种六十面体。其具有互相相交的面，是一种复杂多面体，但其仅有面互相相交，其所有面都是凸多边形。

外观

大五角化十二面体也可以视为在大十二面体向内侧叠上五角锥所形成的立体

大五角化十二面体的外观与在正十二面体的每个面上叠上锥高非常高、非常尖锐的五角锥相同，但若只是在正十二面体的每个面上叠上五角锥这样的结构与大五角化十二面体的拓扑结构并不相同，大五角化十二面体除了露在立体外部可见的12个尖锐角之外，还有12个顶点隐没在立体内部，这12个顶点在立体内部与等腰三角形的底边形成一个正二十面体，若检视每个叠上的锥体之底面的配置，则在立体内部由等腰三角形底边构成的结构可以视为一个大十二面体，这些顶点都是10个等腰三角形底角的公共顶点，顶点图为施莱夫利符号计为{10/3}的十角星，对应其对偶多面体的十角星面，而这个立体露在外部的12个尖角则对应其对偶多面体的五边形面，因此，大五角化十二面体的对偶多面体是一个由12个十角星和12个五边形组成的多面体。

面的组成

大五角化十二面体的面由60个全等的等腰三角形组成，每个等腰三角形彼此互相相交，每个等腰三角形皆露出一个角，其余两角皆隐藏于该立体的内部。露在该立体外部的部分如下图，以蓝色表示，其中黑线代表等腰三角形彼此互相相交的位置：

若大五角化十二面体的对偶多面体——小星形截角十二面体的边长为单位长，则对应的大五角化十二面体的短边长，也就是等腰三角形的底边长为：

${\frac {3{\sqrt {5}}-5}{2}}\approx 0.8541019662$

大五角化十二面体的长边长，也就是等腰三角形的腰长为：

${\frac {5\left(1+{\sqrt {5}}\right)}{2}}\approx 8.0901699437$

由此可得到大五角化十二面体其顶角约为6度，这个角为大五角化十二面体十分锐利的尖角：

$\arccos({\frac {1}{10}}+{\frac {2}{5}}{\sqrt {5}})\approx 0.105621899\approx 6.051\,689\,017\,91^{\circ }$

等腰三角形的另外两个底角为：

$\arccos({\frac {1}{2}}-{\frac {1}{5}}{\sqrt {5}})\approx 1.51798538\approx 86.974\,155\,491\,04^{\circ }$

二面角

大五角化十二面体有两种二面角，一种为等腰三角形的底边与等腰三角形的底边的二面角，另一种为等腰三角形的腰与腰的二面角。这两种二面角的角度相等，其值为：

$\arccos({\frac {-24+5{\sqrt {5}}}{41}})\approx 1.88880388\approx 108.220\,490\,680\,83^{\circ }$

顶点的组成

大五角化十二面体有两种顶点，分别为5个等腰三角形顶角的公共顶点和10个等腰三角形底角的公共顶点。其中5个等腰三角形顶角的公共顶点露在立体外部，为大五角化十二面体最明显的12个五角化十二面体之尖角，另外12个等腰三角形底角顶点隐没于立体内部。其中，露在立体外部的12个尖角的顶点座标为：

$\left(0,\,\pm {\frac {5\left(3+{\sqrt {5}}\right)}{4}},\,\pm {\frac {5\left(1+{\sqrt {5}}\right)}{4}}\right)$

$\left(\pm {\frac {5\left(3+{\sqrt {5}}\right)}{4}},\,\pm {\frac {5\left(1+{\sqrt {5}}\right)}{4}},\,0\right)$

$\left(\pm {\frac {5\left(1+{\sqrt {5}}\right)}{4}},\,0,\,\pm {\frac {5\left(3+{\sqrt {5}}\right)}{4}}\right)$

隐没于立体内部的12个顶点座标为：

$\left(0,\,\pm {\frac {5-{\sqrt {5}}}{4}},\,\pm {\frac {3{\sqrt {5}}-5}{4}}\right)$

$\left(\pm {\frac {5-{\sqrt {5}}}{4}},\,\pm {\frac {3{\sqrt {5}}-5}{4}},\,0\right)$

$\left(\pm {\frac {3{\sqrt {5}}-5}{4}},\,0,\,\pm {\frac {5-{\sqrt {5}}}{4}}\right)$

相关多面体

各种五角化后的正十二面体变种连续动画。动画中依序展示了正十二面体（原像）、五角化十二面体、菱形三十面体、小星形十二面体、大五角化十二面体、复合大三角六边形二十面体凹五角锥十二面体与凹五角锥十二面体等形状

在外观上，大五角化十二面体形似在正十二面体的每个面上叠上锥高非常高的五角锥所构成的立体，依照不同的锥高可以得到不同的立体。

图像	名称	加入锥体的方式	锥高
	复合大三角六边形二十面体凹五角锥十二面体	加入倒五角锥并从另外一侧穿出
	凹五角锥十二面体	加入倒五角锥
	正十二面体	原始形状	0
	五角化十二面体	加入到能使所有二面角等角的高度	0.251 ${\frac {1}{{\sqrt {1+{\frac {1}{\varphi ^{2}}}}}\left(3+{\frac {1}{\varphi ^{2}}}\right)}}$
	菱形三十面体	加入到面两两共面的高度	0.425 ${\frac {a}{2{\sqrt {1+{\frac {1}{\varphi ^{2}}}}}}}$
	小星形十二面体		1.37638 ${\sqrt {{\tfrac {1}{5}}\left(5+2{\sqrt {5}}\right)}}$
	大五角化十二面体	这些看似叠在正二十面体表面的锥体实际上其底面在可见的正十二面体内部构成一个大十二面体。

参考书目

• Wenninger, Magnus, Dual Models, Cambridge University Press, 1983, ISBN 978-0-521-54325-5, MR 0730208 

外部链接

• 埃里克·韦斯坦因. 大五角化十二面體. MathWorld.