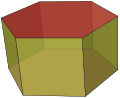
双锥体
(重定向自雙稜錐)
双锥体,或双棱锥、又称双角锥,是一种几何体,是由一锥体,经底面镜射产生的像和原本的锥体合成的立体,换句话说,双锥体就是将两个相同的锥体背对背、底面对底面黏起来。其也是柱体的对偶多面体,将一柱体每面的重心当作新的顶点做成多面体也可得到双锥体。
 以双六角锥为例 | |||
| 类别 | 双锥体 | ||
|---|---|---|---|
| 对偶多面体 | n角柱 | ||
| 数学表示法 | |||
| 考克斯特符号 | |||
| 施莱夫利符号 | { } + {n} | ||
| 性质 | |||
| 面 | |||
| 边 | |||
| 顶点 | |||
| 欧拉特征数 | F=, E=, V= (χ=2) | ||
| 组成与布局 | |||
| 面的种类 | 三角形 | ||
| 顶点图 | V4.4.n | ||
| 对称性 | |||
| 对称群 | Dnh, [n,2], (*n22), order 4n | ||
| 旋转对称群 | Dn, [n,2]+, (n22), order 2n | ||
| 特性 | |||
| 凸、 面可递 | |||
| 图像 | |||
| |||
| 注:为底面边数 。 | |||
体积
编辑双锥的体积 ,其中B是中央切面的面积,基座的面积;h是基座到顶点的高度。
正双锥的体积,基座的正n边形长度为s,基座到顶点的高度为h,则有:
詹森双锥
编辑在所有双锥中,有3个双锥全部都由正多边形组成,分别为双三角锥、双四角锥和双五角锥;双六角锥退化成一个平面。
双三角锥和双五角锥属于詹森多面体;双四角锥属于正多面体,因此不属于詹森多面体。
| 双三角锥 | 双四角锥 (正八面体) |
双五角锥 |
参考来源
编辑- 埃里克·韦斯坦因. Dipyramid. MathWorld.
- Olshevsky, George, Bipyramid at Glossary for Hyperspace.
- The Uniform Polyhedra (页面存档备份,存于互联网档案馆)
- Virtual Reality Polyhedra (页面存档备份,存于互联网档案馆) The Encyclopedia of Polyhedra
- VRML models (George Hart) (页面存档备份,存于互联网档案馆) <3> (页面存档备份,存于互联网档案馆) <4> (页面存档备份,存于互联网档案馆) <5> (页面存档备份,存于互联网档案馆) <6> (页面存档备份,存于互联网档案馆) <7> <8> (页面存档备份,存于互联网档案馆) <9> (页面存档备份,存于互联网档案馆) <10> (页面存档备份,存于互联网档案馆)
- Conway Notation for Polyhedra (页面存档备份,存于互联网档案馆) Try: "dPn", where n = 3, 4, 5, 6, ... example "dP4" is an octahedron.
- VRML models (George Hart) (页面存档备份,存于互联网档案馆) <3> (页面存档备份,存于互联网档案馆) <4> (页面存档备份,存于互联网档案馆) <5> (页面存档备份,存于互联网档案馆) <6> (页面存档备份,存于互联网档案馆) <7> <8> (页面存档备份,存于互联网档案馆) <9> (页面存档备份,存于互联网档案馆) <10> (页面存档备份,存于互联网档案馆)