维基百科

宇宙距离尺度

天體物理學測量方法
关于宇宙学中距离的各种定义，请见“距离测量 (宇宙学)”。

宇宙距离阶梯（也称为银河系外星系距离尺度）是天文学家用以决定天体距离的一系列方法。只有那些距离地球“足够近”（大约在一千秒差距内）的天体，才有可能直接量测距离。测量更遥远天体距离的技术，都是奠基于对近距离天体量测方法之间的关联。有几种方法依赖标准烛光：已知光度的几种天体。

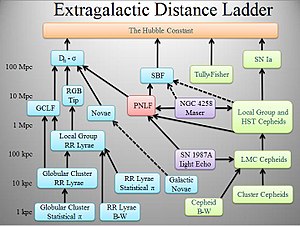
阶梯类比之所以出现，是因为没有一种技术可以量测天文学中的所有长度。天文学家采用了复合方案来替代，有方法可以量测附近天体的距离，也有另一种方法可以量测距离稍远一点的天体，还有一种方法可以量测距离更远一点的天体，依此类推。这就像阶梯一样，每一阶都能升到更高；每种方法与前一种都会有重叠的部分，因此前一种方法可以为下一种方法提供校准，让天文学家可以测量出越来越遥远天体的距离。

直接测量法

编辑
 
在澳洲首都领地堪培拉国家科技馆（英语：Questacon），此雕像“天文学家”展现了使用视差法来测量距离。这是利用耶鲁-哥伦比亚折射镜（望远镜，c1925）的方位圈和烧毁的其它部分制造的。这架望远镜原本安装在斯壮罗山天文台，于2003年堪培拉大火被烧毁

在阶梯的最底部是最基本的距离测量法，这些方法没有对观测天体做任何物理假设，而是直接测量距离。精确测量恒星位置是天体测量学的一部分。

天文单位

编辑
主条目：天文单位

天文单位，即地球和太阳之间的平均距离，是直接测量法的基础。开普勒定律提供了不同绕日物体间的精确轨道大小比值，但没有提供轨道整体大小的量测。雷达用来量测地球轨道和另一天体轨道的距离。根据此测量值和精确的行星轨道距离比，可计算出地球轨道的大小。地球轨道的精确度已经达到数米的等级，相当于精确度达到千亿分之一(1×10−11)。

历史上，金星凌日的观测对确定天文单位至关重要；在20世纪前半段，观测小行星也很重要。目前地球轨道的高精度测量，是使用雷达测量地球与金星和其他接近地球的小行星的距离[1]，还有追踪在轨道上环绕太阳和在太阳系行星间空间运行的太空船。

视差

编辑
主条目：视差
参见：恒星视差和秒差距
 
恒星视差是地球周年运动引起的视差。视差角是顶角的一半

源自三角学的视差是量测距离最重要的基础。当地球绕太阳运行时，附近恒星的位置会在较远的背景上发生轻微的移动。这个位移的角度是一等腰三角形的顶角，等腰三角形的底边为2天文单位 （地球绕太阳轨道的极端位置间的距离），腰边为恒星与地球间的距离。这个位移相当小，并且随着距离的增加而减少。1角秒的变化相当1秒差距（3.26光年）的距离。天文学家通常用秒差距来表示距离；在一般的场合与媒体上则流行用光年。

由于距离越远视差的值越小，所以只适用于测量邻近地球的恒星。这些恒星必须要足够近，其视差角才会在测量精度之上。视差测量只能达到毫弧秒的精确度[2]。在1990年代，例如依巴谷卫星任务，获得超过10万颗恒星的视差，精度约1毫弧秒[3]，提供有用的恒星距离为数秒差距到数百秒差距。现在，哈伯太空望远镜的第三代广域照相机（WFC3）有可能提供20到40微弧秒的精确度，从而使少数恒星的可靠距离测量达到5,000秒差距（16,000光年）[4][5]。在2018年，来自盖亚任务发布的第二批资料，对大多数比视星等15等更亮的恒星，可以达到同样的距离精确度[6]。

恒星相对于太阳的运动导致自行（横向跨越天空）和径向速度（朝向或远离太阳的运动）。前者可以通过绘制恒星在许多年中的位置变化来确定，后者则测量沿视线运动引起的恒星光谱多普勒位移得到确认。对有着相同光谱类型与相似星等范围的一群恒星，可以从相对于自行与迳向速度的统计分析得到平均视差。 统计视差这种方法，对于距离超过50秒差距的亮星和包括造父变星和天琴座RR型变星等明亮的变星，都非常有用[7]。

 
视差测量可能是了解宇宙中最难以捉摸的三个组成部分：暗物质、暗能量和微中子的重要线索[8]
 
哈伯精密的距离测量，已将银河系中可以测量的恒星距离扩展了10倍[9]

太阳在空间中的运动提供了一条更长的基线，可以增加视差法的准确性，称为长期视差法。对于银河盘面中的恒星，这相当于每年平均4天文单位的基线，对银晕中的恒星是每年40天文单位。经过数十年，这个基线可比传统视差法使用的日地基线高出几个数量级。不过，因为观察天体的相对速度未知，长期视差法的不确定性也随之上升。当应用在多恒星的样本时，因为精确度反比于样本数量大小的平方根，可以减少不确定性 [10]。

移动星团视差法，是由在邻近的星团中的一颗恒星的运动，来测量星团距离的一种技术。只有疏散星团的距离近到可以使用这种方法。特别是毕宿星团的距离测量，在历史上是距离阶梯中重要的一步。

在特殊的情况下，可以对个别的其它天体进行基本的距离估计。如果一个扩张中的气体云，像是超新星残骸或行星状星云，在观察一段时间之后，可以根据扩张视差估计其距离。但是这样的测量会因观测物体偏离球形而有误差。联星，若同时是视联星和光谱联星，也可以通过类似的方法估计它们的距离，并且没有前述几何学上的不确定性。这些方法的共同特性是在测量上结合了角运动与绝对速度（通常是通过观察多普勒效应）。可计算物体要多远，才能以这样的绝对速度下显示出观察到的角运动，来得到物体的距离。

特别的是膨胀视差可以给出非常遥远天体的基本距离估计，这是因为超新星的喷发物有着很大的扩张速度和尺寸（相较于恒星）。此外，可以用电波干涉仪测量非常小的角运动。结合这些，可以经由对超新星的测量，做为估计其宿主星系距离的基础测量[11]。膨胀视差虽然有价值，但却非常罕见。所以它们经常是做为距离阶梯上重要的验证工具，而不是测量距离本身的主要工具。

标准烛光法

编辑

几乎所有用来做为距离指标的天体，都属于具有已知亮度的类形。通过将比较已知的光度与观察天体所得的亮度，可以使用平方反比定律计算出天体的距离。这些已知亮度的天体被称为"标准蜡光" ，由亨丽埃塔·史旺·勒维特所引入。[12]

天体的亮度可以用其绝对星等来表示。这个量是从10秒差距的距离观察所得光度的对数导出的。视星等是观测者所看到的亮度（使用的仪器是辐射热测量计），可用来与绝对星等一起来计算出数秒差距内的天体的距离，公式如下：

 

或

 

此处，m是视星等，M是绝对星等，d是距离。这个结果要准确，视星等与绝对星等的测量波段要相等，且该天体在径向（视线方向）上无相对运动。

一些修正，像是星际消光是必要的。星际消光会使天体看起来黯淡和偏红，特别是对位于满是灰尘或气体区域方向上的天体[13]。天体的视星等和绝对星等之间的差别叫做距离模数，天文上的距离，特别是星系际的，有时会以两者并列的方式呈现。

问题

编辑

所有标准烛光法都有两个问题。主要的一个问题是校准，就是如何确定标准烛光的绝对星等。这包括定义的类别要有足够多的成员可供识别，并且能够发现足够多的距离和绝对星等都够精确的成员。第二个问题是同类成员的辨识，而不是错误的使用不属于该类天体的标准烛光来校准。在最极限的距离，也就是最希望可作为距离指标的距离，识别问题可能会相当的严重。

标准烛光主要的一个重大议题是它们到底有多标准的质疑不断出现。例如，所有的观测似乎都表明，已知距离的Ia超新星具有相同的亮度（经光变曲线修正后）。距离与亮度的密切关系下方有详述。然而，距离遥远的Ia超新星与邻近的Ia超新星可能有着不同的性质。使用Ia超新星在确定宇宙模型时至关重要。如果在远处的Ia超新星真的有着不同的性质。也就是说，如果将校准外推到任意距离上是不正确的，忽略这种变化可能会严重的危害到宇宙参数的重建，特别是在物质密度参数的重建[14][需要解释]。

从使用造父变星测量距离的历史来看，这不只是一个哲学上的设想问题。在1950年代，沃尔特·巴德发现，做为标准烛光校准的造父变星，在近距离的类型与用来测量邻近星系距离的是不同类型。附近的造父变星是第一星族星，比远处的第二星族星有着较高的金属量。结果是，第二星族星实际上比人们所认为的还要明亮；在修正后，球状星团和邻近星系的距离，以及银河系的直径都倍增了。

标准警铃

编辑

致密双星的旋近所发射出的引力波拥有某些很有用的特性，例如，这种引力波的波强与波型强烈地与双星系统的啁啾质量有关。从观测波型，可以准确地估算出啁啾质量。知道啁啾质量与观测到的波强，就可以给出波源距离。由于引力波不会因传播途中的宇宙介质而被消光，因此，引力波源是标准警铃，其不需要宇宙距离梯度，也不需要实验校准，只需要假定广义相对论正确无误。.[15][16]

假若引力波事件也可以用光学探测器观察到，则可以从观察到的电磁辐射的多普勒红移估算出哈勃常数。[17]

标准尺

编辑

另一类物理距离指标是标准尺。在2008年，宇宙学的参数测量似乎可以给出星系直径的标准尺[18]。这个方法利用在宇宙早期的重子声学振荡（BAO，baryon acoustic oscillation）：在原始等离子中的声学振荡幅度不会超过在所有的尺度内都存在的小结构尺度。然后，在等离子中的非均质性促成重力组织了丝状结构和空洞。因此，宇宙的空洞尺度不会超过BAO能够给予它们的大小。这种方法需要广泛的调查星系才能看出其尺度。为测量暗能量扩张效应的WiggleZ星系巡天能够解决这种尺度。

光回波也可以作为标准尺。

星系距离指标

编辑
参见：距离测量 (宇宙学)

除了少数例外，以直接测量为基础的距离只到在千秒差距，这仍被限制在我们的银河系之内。超过这个之外的距离，测量是依据物理学上的假设，也就是，这一类天体的分布是足够均匀的，因此以这些成员用于估计距离是有意义的。

物理学的距离指标，使用在日益增大的距离尺度，包括：

主序星拟合

编辑

当一群恒星的绝对星等被描绘成赫罗图相对于恒星的光谱类型，就能发现相对于质量、年龄、和组成的恒星演化模式。在实务上，当氢燃烧的期间，恒星的分布的曲线在图中称为主序带。通过测量这些恒星光谱的属性，可以在赫罗图上确定恒星在主序带上的位置，并从而估计出恒星的绝对星等。比较视星等和绝对星等的差值，再经过因为气体和尘埃对亮度造成的星际消光修正，就可以逼近要测定的距离。

在受到重力约束的星团，像毕宿星团，恒星形成的年龄相近，而且有着相近似的距离。这允许相对来说更精确的主序星拟合，提供年龄和距离的测定。

系外星系距离尺度

编辑
系外星系距离指标[22]
方法 不确定的单独星系（星等） 至室女座星系团的距离（Mpc） 范围（Mpc）
古典造父变星 0.16 15 - 25 29
新星 0.4 21.1 ± 3.9 20
行星状星云亮度函数 0.3 15.4 ± 1.1 50
球状星团亮度函数 0.4 18.8 ± 3.8 50
表面亮度波动 0.3 15.9 ± 0.9 50
D - σ关系 0.5 16.8 ± 2.4 > 100
Ia型超新星 0.10 19.4 ± 5.0 > 1000

河外星系距离规模是今天的天文学家用来确定超越我们银河系的宇宙，以传统方法不容易获得距离的一系列技术。有些程序利用到某些的天体特性，像是恒星、球状星团、星云和整个的星系。其它的方法是基于更多的统计和概率的事情，像是整个星系团。

威尔逊-巴甫效应

编辑
主条目：威尔逊-巴甫效应

利用已知的分光视差效应，奥林·威尔逊和外努·巴甫（英语：Vainu Bappu）在1956年发现威尔逊-巴甫效应。某些恒星在它们的吸收/发射谱线上有着容易计算绝对星等的特征点；有些谱线直接显示天体的大小，像是钙的K吸收线。利用距离模数可以从星等计算恒星的距离：

 。

虽然理论上这种方法可以计算的距离可以达到700万秒差距，但通常只能应用在数十万秒差距远的恒星。

这种方法只适用比15等亮的恒星。

古典造父变星

编辑

超越威尔逊-巴甫效应，下一种方法依赖古典造父变星周光关系，这是亨丽爱塔·勒维特首度发现的。下面的关系式可以用来计算银河系和河外星系的古典造父变星距离：

 。[23]

有几个问题使造父变星作为标准烛光的运用变得复杂，并引发积极的辩论，其中主要有：天然和线性周光关系的零点和斜率两者都会受到金属量的冲击和通过频带的影响，光度计的污染（材质）和造父变星在距离上的因消光（通常是未知的）产生的变化等造成的影响[24][25][26][27][28][29][30][31][32]。

这些未解决的问题导致在测距时引用的哈伯常数数值在60km/s/Mpc和80km/s/Mpc之间。解决此一差异是天文学的首要问题之一，从宇宙的宇宙参数或许勉强可以提供更精确的哈伯常数值[33][34]。

造父变星是爱德温哈伯在1923年得到仙女座星系是河外星系，不是银河系内相对较小星云的关键工具。它当时计算M31的距离是285,000秒差距，今天的距离是770,000秒差距。

当检测更遥远的距离，在狮子座内的螺旋星系NGC 3370，有着迄今发现距离最远的变星，2,900万秒差距。造父变星没有变法完美的指示距离：近距离的星系误差可以达到7%，最远的误差达到15%。

超新星

编辑
 
在星系NGC 4526（左下的亮点）的超新星SN 1994D。影像由NASA、ESA、哈伯关键计划团队、和高Z超新星搜寻团队

有几种不同的方法可以用超新星测量距离，在这里介绍的是最常用的。

测量超新星的光球层

编辑

我们可以假设一颗扩张中的超新星是球对称的。如果这颗超新星的距离够近，则我们可以测量光球层扩张的角度，θ（t），我们可以使用公式：

 。

此处ω是角速度，θ是扩张的角度。为了获得精确的测量，有必要以Δt的间隔在不同的时间观测，我们可以利用

 。

此处d是超新星的距哩，Vej超新星喷发物的径向速度（如果是球对称，可以假设Vej'等于Vθ）。

这种方法只有在超新星够接近时才能使用，以便能准确的测量光球。同样的，气体壳的膨胀事实上暨不是完美的球对称，也不是完美的黑体。此外，星际消光也会妨碍光球测量的精确度。这些问题因为超新星的核心塌缩会进一步的恶化。所有这些因素使得距离的误差会高达25%。

Ia型超新星光度曲线

编辑

Ia型超新星是确定星系距离最好的方法之一。当一颗白矮星开始从伴星的红巨星吸积质量时，就会启动产生Ia型超新星的过程，白矮星的质量最终会达到钱德拉塞卡极限，即 。

这时，这颗白矮星会变得不稳定，并经历失控的核聚变反应。因为所有的Ia型超新星都在相同的质量下爆炸，因此绝对星等几乎都一样。这造成了非常有用的标准烛光，所有的Ia型超新星有着相同的颜色——蓝色和可见光星等

 。

因此，当观测到爆发中的Ia型超新星，如果可以测到它的峰值星等，就可以计算出距离。这并不需要实质上直接补获超新星在峰值时的规模，使用多色光度曲线形状法（MLCS），将光度曲线的形状（在初始爆炸之后合理的时间内）与绝对星等参数化的家族曲线比较以确定最大亮度。这种方法也需要考虑到来自气体和尘埃的星际消光。

同样的，延伸法的光度曲线范本适合特定的超新星星等光度曲线。这个范本，相对于不同的波长（MLCS）只是一些在时间上被延伸（压缩）的不同光度曲线。通过使用延展因数，可以测量出星等的峰值[来源请求]。

使用Ia型超新星是最准确的方法之一，特别是因为在遥远星系的超新星，比造父变星更远上500倍的距离，也可以被看见（它们的光度可以与所在的星系匹敌）。天文学家花了许多时间淬炼这种方法，目前的误差只有5%，相当于0.1星等的不确定性。

新星测量距离

编辑

也可以用与超新星非常相似的方法，用新星导出河外星系的距离。这是新星的最大光度与可见光的光度下降2星等时间的直接关系。它们的关系如下：

 。

此处 是新星星等延伸的时间，描述的是最初2星等的下降平均率。

在新星暗淡之后，它们的亮度大约与最亮的造父变星相同，因此这两种方法可以测量的最大距离相同，大约都是2,000万秒差距。这种方法在星等上的误差大约是± 0.4。

球状星团亮度函数

编辑

以来自室女座星系团的遥远星系，比较球状星团（位于星系晕）光度为基础的方法，球状星团亮度函数带有的不确定性大约是20%（或0.4星等）。

美国天文学家威廉·阿尔文·鲍姆首度试图用球状星团测量椭圆星系的距离。他假设星系中最亮的球状星团有着相同的亮度，比较室女座A星系和仙女座星系中最亮的球状星团。知道仙女座星系的距离，他假设有值接的关联性，就可以估计室女座A的距离。

鲍姆只使用单一的球状星团，但个别的单位往往欠缺标准烛光。加拿大天文学家拉辛使用球状星团亮度函数（GCLF，the globular cluster luminosity function）可以导出更好的近似值。球状星团亮度与星等的函数关系值如下：

 。

此处m0折让星等，M0是室女座球状星团的星等，σ分散~ 1.4星等。

很重要的是必须记住他的假设是在宇宙中所有的球状星团有着大约相同一致的光度。没有通用的球状星团发光函数能适用于所有的星系。

行星状星云亮度函数

编辑

类似于GCLF法，相似的数值分析可以使用在遥远星系内的行星状星云（注意要使用多个）。荷兰·科尔和大卫·詹纳在1970年代末期首次提出行星状星云亮度函数（PNLF）。他们建议所有的行星状星云有着相似的最大本质亮度，现在的计算是M = -4.53。这会使它们成为潜在的确河外定星系距离的标准烛光。

天文学家George Howard Jacoby和他在学院的伙伴，稍后提出PNLF函数方程式的等式：

 。

此处N（M）是行星状星云的数量，有着绝对星等M。M*相当于是星等最亮的星云。

表面亮度起伏法

编辑
 
星系团

下面的方法处理的是星系整体的固有属性。这些方法，虽然有不同的误差百分比，但是有能力估计1亿秒差距以外的距离，不过仍是较常应用在银河系内。

表面亮度起伏（SBF）法需要利用装在望远镜上的CCD相机。在星系表面的亮度因为在空间起伏，相机中的一些图元接收到的星星将会比其它的图元多。但是，随着距离的增加图像会变得越来越平滑。分析从一个图元致另一个图元的星等变化直接关系到星系的距离。

D-σ关系

编辑

D-σ关系，使用在椭圆星系，将椭圆星系的角直径（D）和速度弥散度联系在一起。为了了解这种方法。精确的描述D的内容是很重要的。更精确的说，它是以20.75B星等弧 水准的星系角直径导出表面亮度。这种表面亮度与星系至我们的实际距离无关。相反的，D是与星系的距离成反比，以d表示。因此，这种关系不会被当成标准烛光；相反的，D提供了标准尺。D和σ的关系是

 。

此处，C是一个取决于星系团距离的常数。

这种方法有可能成为最强的星系距离计算工具，也许会超过塔利-费舍尔关系的方法。然而迄今，椭圆星系还不足以提供足够的亮度通过其它的技术来校准，例如造父变星。相反的，使用更多粗糙（原生）的方法来完成校准。

重叠和提升

编辑

一连串的距离指标，像是距离的阶梯，须要能确定至其它星系的距离。原因是这些天体的亮度在这些距离上可以辨识和测量，但是在近距离却是罕见或是完全没有，由于距离近到可以作为三角视差校准指标的例子太少。例如，造父变星，是在邻近的螺旋星系中最佳的距离指标之一，但不能满意的单独由视差来校准。不同的族群中不能拥有所有不同类型的恒星，使形势进一步的复杂化。造父变星是独特的大质量恒星，生命期短，所以它们只能在最近还有恒星形成的地方被发现。结果是，因为椭圆星系通常没有大规模的恒星形成，所以那儿没有造父变星。取代的是，必须使用老年恒星的族群（像是新星和天琴座RR变星）。但是天琴座RR变星不若造父变星般明亮（所以不能如造父变星在那么远的距离上被看见），而新星在程序上是不可预知的，需要细致－和好运气－的监控程式，在目标星系中观测到足够多的新星，才能很好的估计距离。

因为距离更远的宇宙阶段的阶梯决于近距离的阶梯，更远的阶段的，包括系统的和统际的误差，都会受到较近阶梯误差的影响。结果是，这些误差传播的结果意味着天文学上的距离很少会和其他科学的同级别在测量上有着相同的精确度，各类型的天体距离越遥远精确度也就越低。

另一个关注的问题，尤其是对非常明亮的标准烛光，是它们的"标准"：它们的绝对星等同质性是怎样的规模。对于这一些不同的标准烛光，有些的同质性是基于恒星形成的理论和星系和恒星演化，因此在这些主题方面的因素也是不确定的。对最明亮的距离指标，Ia型超新星，它们的同质性是很贫乏的[来源请求]；然而，没有其他类别的天体是亮到族已验证如此遥远的距离，所以使用这样的类别只是因为没有其他的可以选择。

哈伯定律是观测的结果，星系远离我们而去的距离和速度的比率是宇宙距离阶梯的产品。哈伯观测到越暗淡的星系有越大的红移。发现哈伯常数的值，是许多天文学家在假设和测量星系红移与校准宇宙距离阶梯上，工作数十年的结果。哈伯定律的主要意义是我们估计类星体的距离和星系的距离，是无法用个别的指标得到结果的。

相关条目

编辑

参考资料

编辑
  1. ^ Ash, M. E.; Shapiro, I. I.; Smith, W. B. Astronomical constants and planetary ephemerides deduced from radar and optical observations. The Astronomical Journal. 1967, 72: 338. Bibcode:1967AJ.....72..338A. doi:10.1086/110230. 
  2. ^ Staff. Trigonometric Parallax. The SAO Encyclopedia of Astronomy. Swinburne Centre for Astrophysics and Supercomputing. [2008-10-18]. （原始内容存档于2008-07-28）. 
  3. ^ Perryman, M. A. C.; et al. The HIPPARCOS Catalogue. Astronomy and Astrophysics. 1999, 323: L49–L52. Bibcode:1997A&A...323L..49P. 
  4. ^ Harrington, J. D.; Villard, R. NASA's Hubble Extends Stellar Tape Measure 10 Times Farther Into Space. NASA. 10 April 2014 [17 October 2014]. （原始内容存档于2019-02-17）. 
  5. ^ Riess, A. G.; Casertano, S.; Anderson, J.; MacKenty, J.; Filippenko, A. V. Parallax Beyond a Kiloparsec from Spatially Scanning the Wide Field Camera 3 on the Hubble Space Telescope. The Astrophysical Journal. 2014, 785 (2): 161. Bibcode:2014ApJ...785..161R. arXiv:1401.0484  . doi:10.1088/0004-637X/785/2/161. 
  6. ^ Brown, A. G. A.; Vallenari, A.; Prusti, T.; de Bruijne, J. H. J.; et al. Gaia Data Release 2. Summary of the contents and survey properties. Astronomy & Astrophysics. 2018. Bibcode:2018A&A...616A...1G. arXiv:1804.09365  . doi:10.1051/0004-6361/201833051. 
  7. ^ B., Baidyanath. An Introduction to Astrophysics. PHI Learning Private Limited. 2003. ISBN 81-203-1121-3. 
  8. ^ Hubble finds Universe may be expanding faster than expected. [3 June 2016]. （原始内容存档于2018-09-11）. 
  9. ^ Hubble stretches the stellar tape measure ten times further. ESA/Hubble Images. [April 12, 2014]. （原始内容存档于2017-10-30）. 
  10. ^ Popowski, P.; Gould, A. Mathematics of Statistical Parallax and the Local Distance Scale. 1998. arXiv:astro-ph/9703140  . 
  11. ^ Bartel, N.; et al. The shape, expansion rate and distance of supernova 1993J from VLBI measurements. Nature. 1994, 368 (6472): 610–613. Bibcode:1994Natur.368..610B. doi:10.1038/368610a0. 
  12. ^ Fernie, J. D. The Period-Luminosity Relation: A Historical Review. Publications of the Astronomical Society of the Pacific. December 1969, 81 (483): 707. Bibcode:1969PASP...81..707F. ISSN 0004-6280. doi:10.1086/128847  . 
  13. ^ Type Ia Supernova. Weekly Topic. Caglow. [30 January 2012]. （原始内容存档于2012-02-29）. 
  14. ^ Linden, S.; Virey, J.-M.; Tilquin, A. Cosmological parameter extraction and biases from type Ia supernova magnitude evolution. Astronomy and Astrophysics. 2009, 506 (3): 1095–1105. Bibcode:2009A&A...506.1095L. arXiv:0907.4495  . doi:10.1051/0004-6361/200912811.  (And references therein.)
  15. ^ Hendry, Martin; Woan, Graham. Gravitational astrophysics. Astronomy & Geophysics. February 2007, 48 (1): 1.10–1.17 [October 16, 2017]. Bibcode:2007A&G....48a..10H. doi:10.1111/j.1468-4004.2007.48110.x. （原始内容存档于2017-10-17）. 
  16. ^ Holz, Daniel; Hughes, Scott; Shultz, Bernard. Measuring cosmic distances with standard sirens. Physics Today. 2018, 71 (12): 35–40. doi:10.1063/PT.3.4090. 
  17. ^ Abbott, B. P.; et al. A gravitational-wave standard siren measurement of the Hubble constant. Nature. 16 October 2017, 551 (7678): 85–88 [2018-12-18]. Bibcode:2017Natur.551...85A. PMID 29094696. arXiv:1710.05835  . doi:10.1038/nature24471. （原始内容存档于2019-12-23）. 
  18. ^ 引用错误：没有为名为Marinonietal2009的参考文献提供内容
  19. ^ Bonanos, Alceste Z. Eclipsing Binaries: Tools for Calibrating the Extragalactic Distance Scale. Binary Stars as Critical Tools and Tests in Contemporary Astrophysics, International Astronomical Union. Symposium no. 240, held 22–25 August 2006 in Prague, Czech Republic, S240, #008. 2006, 2: 79–87. Bibcode:2007IAUS..240...79B. arXiv:astro-ph/0610923  . doi:10.1017/S1743921307003845. 
  20. ^ Ferrarese, Laura; Ford, Holland C.; Huchra, John; Kennicutt, Robert C., Jr.; Mould, Jeremy R.; Sakai, Shoko; Freedman, Wendy L.; Stetson, Peter B.; Madore, Barry F.; Gibson, Brad K.; Graham, John A.; Hughes, Shaun M.; Illingworth, Garth D.; Kelson, Daniel D.; Macri, Lucas; Sebo, Kim; Silbermann, N. A. A Database of Cepheid Distance Moduli and Tip of the Red Giant Branch, Globular Cluster Luminosity Function, Planetary Nebula Luminosity Function, and Surface Brightness Fluctuation Data Useful for Distance Determinations. The Astrophysical Journal Supplement Series. 2000, 128 (2): 431–459. Bibcode:2000ApJS..128..431F. arXiv:astro-ph/9910501  . doi:10.1086/313391. 
  21. ^ S. A. Colgate. Supernovae as a standard candle for cosmology. Astrophysical Journal. 1979, 232 (1): 404–408. Bibcode:1979ApJ...232..404C. doi:10.1086/157300. 
  22. ^ Adapted from Jacoby et al., Publ. Astron. Soc. Pac., 104, 499, 1992
  23. ^ Assessing potential cluster Cepheids from a new distance and reddening parameterization and 2MASS photometry. MNRAS. Bibcode:2008MNRAS.390.1539M. arXiv:0808.2937  . doi:10.1111/j.1365-2966.2008.13834.x. 
  24. ^ Stanek, K. Z.; Udalski, A. The Optical Gravitational Lensing Experiment. Investigating the Influence of Blending on the Cepheid Distance Scale with Cepheids in the Large Magellanic Cloud. Eprint arXiv:astro-ph/9909346. 1999: 9346. Bibcode:1999astro.ph..9346S. arXiv:astro-ph/9909346  . 
  25. ^ Udalski, A.; Wyrzykowski, L.; Pietrzynski, G.; Szewczyk, O.; Szymanski, M.; Kubiak, M.; Soszynski, I.; Zebrun, K. The Optical Gravitational Lensing Experiment. Cepheids in the Galaxy IC1613: No Dependence of the Period-Luminosity Relation on Metallicity. Acta Astronomica. 2001, 51: 221. Bibcode:2001AcA....51..221U. arXiv:astro-ph/0109446  . 
  26. ^ Ngeow, C.; Kanbur, S. M. The Hubble Constant from Type Ia Supernovae Calibrated with the Linear and Nonlinear Cepheid Period-Luminosity Relations. The Astrophysical Journal. 2006, 642: L29. Bibcode:2006ApJ...642L..29N. arXiv:astro-ph/0603643  . doi:10.1086/504478. 
  27. ^ Macri, L. M.; Stanek, K. Z.; Bersier, D.; Greenhill, L. J.; Reid, M. J. A New Cepheid Distance to the Maser-Host Galaxy NGC 4258 and Its Implications for the Hubble Constant. The Astrophysical Journal. 2006, 652 (2): 1133. Bibcode:2006ApJ...652.1133M. arXiv:astro-ph/0608211  . doi:10.1086/508530. 
  28. ^ Bono, G.; Caputo, F.; Fiorentino, G.; Marconi, M.; Musella, I. Cepheids in External Galaxies. I. The Maser-Host Galaxy NGC 4258 and the Metallicity Dependence of Period-Luminosity and Period-Wesenheit Relations. The Astrophysical Journal. 2008, 684: 102. Bibcode:2008ApJ...684..102B. doi:10.1086/589965. 
  29. ^ Majaess, D.; Turner, D.; Lane, D. Type II Cepheids as Extragalactic Distance Candles. Acta Astronomica. 2009, 59: 403. Bibcode:2009AcA....59..403M. 
  30. ^ Madore, Barry F.; Freedman, Wendy L. Concerning the Slope of the Cepheid Period-Luminosity Relation. The Astrophysical Journal. 2009, 696 (2): 1498. Bibcode:2009ApJ...696.1498M. doi:10.1088/0004-637X/696/2/1498. 
  31. ^ Scowcroft, V.; Bersier, D.; Mould, J. R.; Wood, P. R. The effect of metallicity on Cepheid magnitudes and the distance to M33. Monthly Notices of the Royal Astronomical Society. 2009, 396 (3): 1287. Bibcode:2009MNRAS.396.1287S. doi:10.1111/j.1365-2966.2009.14822.x. 
  32. ^ Majaess, D. The Cepheids of Centaurus A (NGC 5128) and Implications for H0. Acta Astronomica. 2010, 60: 121. Bibcode:2010AcA....60..121M. 
  33. ^ Annual Review of Astronomy and Astrophysics. Bibcode:2008A&ARv..15..289T. doi:10.1007/s00159-008-0012-y.  缺少或|title=为空 (帮助)
  34. ^ Annual Review of Astronomy and Astrophysics. Bibcode:2010ARA&A..48..673F. doi:10.1146/annurev-astro-082708-101829.  缺少或|title=为空 (帮助)

书目提要

编辑
  • An Introduction to Modern Astrophysics, Carroll and Ostlie, copyright 2007.
  • Measuring the Universe The Cosmological Distance Ladder, Stephen Webb, copyright 2001.
  • Pasachoff, JM & Filippenko, AV, The Cosmos: Astronomy in the New Millennium（页面存档备份，存于互联网档案馆）, Cambridge: Cambridge University Press, 4th edition, 2013 ISBN 9781107687561.
  • The Astrophysical Journal, The Globular Cluster Luminosity Function as a Distance Indicator: Dynamical Effects, Ostriker and Gnedin, May 5, 1997.
  • An Introduction to Distance Measurement in Astronomy, Richard de Grijs, Chichester: John Wiley & Sons, 2011, ISBN 978-0-470-51180-0.

外部链接

编辑
检索自“https://zh.wikipedia.org/w/index.php?title=宇宙距离尺度&oldid=84515089”