代数记谱法
代数记谱法(Algebraic notation)是国际象棋里用来记录、描述棋子移动的一种方法。目前已成为最普遍的记谱法,所有国际象棋有关的组织、书籍、杂志、报纸都使用这种方法来记谱,最早出现于1173年的波斯象棋。
在英语系国家,自1980年代起,代数记谱法已经取代19世纪常用的描述记谱法,可是描述记谱法在1980~1990之时还是偶而可见到有人使用。欧洲国家除了英国,在代数记谱法被广泛应用之前都是使用描述记谱法。
棋盘上格子的命名法
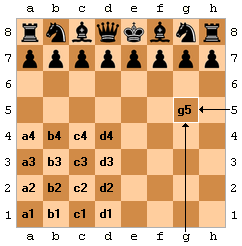
编辑为了便于记录棋谱,棋盘上离白方最近的那一行定为1,最远的那一行定为8。位于白方最左边的那一列定为a,最右边的那一列定为h。这样,白方左下角的第1格的坐标就是a1,白方王所在的原始位置就是e1,黑方后所在的原始位置就是d8。
棋子的命名法
编辑每一个棋子,都分配一个大写字母用作标识,而国际流行的是英文对应单词的首字母,当然这个依不同国家会有所不同(例如法国选手会使用F作为“主教”的缩写,这起源于法语 fou)。按照英文首字母来说,K(King)代表“王”,Q(Queen)代表“皇后”(后),R(Rook)代表“城堡”(车),B(Bishop)代表“主教”(象),N(Knight)代表“骑士”(马)。“兵”通常并不指派字母。
棋子移动的记谱法
编辑棋子的每一步移动都由指示棋子的字母加上目标方格的坐标表示。例如,Be5(象移动到 e5)、Nf3(马移动到f3)。对于兵的移动,不使用指示棋子的字母,仅给出目标方格。例如,c5(兵移动到c5)。
吃子
编辑当一个棋子被吃时,需在目标格子之前添加一个“x”(或乘号“×”)。例如,Bxe5(象吃e5上的棋子)。当一个兵进行吃子时,该兵用吃子前所在的格子的字母代表,例如exd5(格子上的兵吃掉d5上的棋子)。在较早的德语、俄语或意大利语出版物中,有时会使用冒号(:) 来代替“x”,无论是在“x”所在的相同位置(B:e5)还是在末尾(Be5:)。
如果是采用了吃过路兵(法语:en passant)的规则进行吃子的一步,可以在末尾添加“ep”进行强调,也可以不加。如exd6 ep代表e线上的兵吃掉d6的兵。
一些出版物(如《国际象棋开局百科》)在吃子时省略了所有提示(例如,用Be5代替Bxe5;用ed6代替exd6或exd6 ep)。
消除歧义
编辑| a | b | c | d | e | f | g | h | ||
| 8 | 8 | ||||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| a | b | c | d | e | f | g | h | ||
当两个(或更多)相同的棋子都可以移动到同一个格子时,被移动的棋子通过指定棋子的字母来标识唯一,后跟(按优先级降序):
- 出发的格子的字母(如果它们不同);或
- 出发的格子的数字(如果它们不同);或
- 出发的格子的字母以及数字(这仅在很少的情况下发生,即玩家拥有三个及以上相同的棋子(升变造成)可以移动到同一个格子)
在图中,两个黑车都可以合法地移动到f8,因此d8格子上的车到f8的移动被消歧义为Rdf8。对于a线上的两个白车都可以移动到a3,需要提供移动棋子的数字,即R1a3。
在h4上的白后移动到e1的情况下,单独的字母和数字都不足以消除与其他白后的歧义。因此,这一步写成Qh4e1。
如上所述,可以插入“x”和“ep”来表示吃子;例如,如果最后一种情况是吃子,则将其写成Qh4xe1或Qh4xe1 ep。
升变
编辑当棋子升变时,升级成的棋子放移动符号的末尾,例如:e8Q(升级到皇后)。在标准的FIDE符号中,不使用标点符号;在可移植式棋局记号法和许多出版物中,升变由等号 ( 如e8=Q ) 表示。国际象棋文献中使用的其他符号包括括号(例如e8(Q))和正斜杠(例如e8/Q)。
王车易位
编辑王车易位由特殊符号0-0(短易位)和0-0-0(长易位)表示,FIDE标准使用数字0(0-0和0-0-0),PGN则使用字母O(OO和OOO)。[1]
将军
编辑将对手的国王置于将军状态的举动通常附加符号“+”。或者有时会使用匕首(†) 或缩写“ch”。一些出版物用诸如“dis ch”之类的缩写或带有特定符号的方式指示发现的将军。双重将军通常表示与将军相同,但有时被专门表示为“dbl ch”或“++”,特别是在较早的国际象棋文献中。《国际象棋开局百科》全书省略了所有将军指示。
将死
编辑完成移动时的将死由标准FIDE符号和PGN中的符号“#”表示。
表示胜负的记谱法
编辑½–½表示棋赛的结果是和棋。1-0表示棋赛的结果是白方胜。0-1表示棋赛的结果是白方输。
参见
编辑参考文献
编辑- ^ Burgess, Graham. The Mammoth Book of Chess. Carroll & Graph. 2000: 517 [1997]. ISBN 0-7867-0725-9.
外部链接
编辑- FIDE rules on algebraic notation(页面存档备份,存于互联网档案馆)(see appendix C)
- Algebraic Chess Notation Exercise