实际数

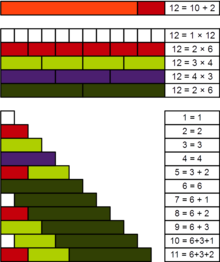
实际数（英语：practical number）是指任意正整数n使得所有小于n的正整数都可以用数个n的相异真因数和表示。例如12的真因数有1, 2, 3, 4及6，而1至11的数字中有几个不是12的真因数，但都可以表示为数个相异真因数的和：5=3+2, 7=6+1, 8=6+2, 9=6+3, 10=6+3+1及11=6+3+2。

通过古氏积木体现12是一个实际数。

以下是实际数的列表（OEIS数列A005153）：1, 2, 4, 6, 8, 12, 16, 18, 20, 24, 28, 30, 32, 36, 40, 42, 48, 54, ....

12,13世纪的义大利数学家斐波那契在其著作《计算之书》（Liber Abaci）中，在说明如何用埃及分数的和表示有理数时有用到实际数。斐波那契没有正式的定义实际数，但其中有一个表，其中有许多分数的分母为实际数。

实际数（practical number）一词最早是由Srinivasan在1948年开始使用，他希望可以找出有这类性质的数字，此工作后来在1955年由Stewart和Sierpiński完成。利用正整数的质因数分解可以判断是否是实际数，所有2的幂及偶数的完全数都是实际数。

已发现实际数和质数有许多类似的特质。

实际数的充份必要条件

一个正整数可以由其质因数分解看出是否是实际数，一正整数$n=p_{1}^{\alpha _{1}}...p_{k}^{\alpha _{k}}$，其中$n>1$，质因数为$p_{1}<p_{2}<\dots <p_{k}$，其为实际数若且唯若$p_{1}=2$，且对于每个2到k之间的i：

$p_{i}\leq 1+\sigma (p_{1}^{\alpha _{1}}\dots p_{i-1}^{\alpha _{i-1}})=1+\prod _{j=1}^{i-1}{\frac {p_{j}^{\alpha _{j}+1}-1}{p_{j}-1}},$

其中$\sigma (x)$为x的除数函数。

例如3 ≤ σ(2)+1 = 4，29 ≤ σ(2 × 3²)+1 = 40，及823 ≤ σ(2 × 3² × 29)+1=1171，因此2 × 3² × 29 × 823 = 429606为一实际数。

由于以上条件成立时，才能用其他较小的因数和表示$p_{i}-1$，因此是一正数为实际数的必要条件。上述条件也是一正数为实际数的充份条件。

和其他数列的关系

所有2的幂都是实际数。2的幂的质因数分解满足实际数的充份必要条件：第一个质因数为2。所有偶数的完全数也都是实际数：依照欧拉的研究，偶数的完全数可以表示为2^n − 1(2ⁿ − 1)，其奇数的质因数可以用其他偶数部份的除数函数来表示，因此也满足实际数的充份必要条件。

任一个质数阶乘也都是实际数。根据伯特兰－切比雪夫定理，质数阶乘中最大的质数会小于次大质数和最小质数（2）的乘积，因此满足实际数的充份必要条件。前k个质数幂次的乘积也都是实际数，包括阶乘以及斯里尼瓦瑟·拉马努金提出的高合成数。

和埃及分数的关系

若n为实际数，则小于1的有理数m/n可以表示∑d_i/n来表示，其中d_i为n的相异因数，此式的每一项都可以化简为单位分数，因此此式即为m/n的埃及分数表示式。例如

${\frac {13}{20}}={\frac {10}{20}}+{\frac {2}{20}}+{\frac {1}{20}}={\frac {1}{2}}+{\frac {1}{10}}+{\frac {1}{20}}.$

斐波那契在其著作《计算之书》（Liber Abaci）中列出许多用埃及分数表示有理数的方式，首先先确认分数是否可以直接化简为单位分数，再来则是设法将分子表示为分母因数的和，此方式只在分母为实际数时有效。斐波那契列出了分母为6, 8, 12, 20, 24, 60及100时，分数用埃及分数表示时的表示式。

和质数的类似之处

实际数特别的一点是其许多性质都类似质数。例如假设p(x)为小于x实际数的个数，Saias证明存在常数c₁及 c₂使得下式成立：

$c_{1}{\frac {x}{\log x}}<p(x)<c_{2}{\frac {x}{\log x}},$

以上公式可以对应素数的素数定理。此证明解答了Margenstern的猜想：存在特定常数c，使得p(x)渐近于cx/log x。也强化了保罗·埃尔德什所提出：实际数在正整数中的密度为0的论点。

实际数也有对应哥德巴赫猜想及孪生质数猜想的定理：每一个偶数可以表示为二个实际数的和，以及存在无限多个 x − 2, x, x + 形式的实际数。Melfi也证明在斐波那契数列中存在无限多个实际数，素数对应的问题是是否存在无限多个斐波那契质数，此问题仍为开放问题，还没有被证明，但也还找不到反例。Hausman及Shapiro证明若x为正实数，在[x²,(x + 1)²]区间内存在实际数，可以对应质数中的勒让德猜想。

外部链接

• Tables of practical numbers （页面存档备份，存于互联网档案馆） compiled by Giuseppe Melfi
• Practical Number at PlanetMath.
• 埃里克·韦斯坦因. Practical Number. MathWorld.