n(A∪B)=n(A)+n(B) -n(A∩B)
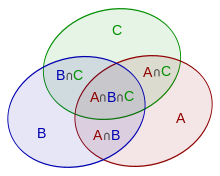
|A∪B∪C|=|A|+|B|+|C|-|A∩B|-|A∩C|-|B∩C|+|A∩B∩C|
要計算幾個集合併集的大小,我們要先將所有單個集合 的大小計算出來,然後減去所有兩個集合相交 的部分,再加回所有三個集合相交 的部分,再減去所有四個集合相交 的部分,依此類推,一直計算到所有集合相交 的部分。
最終得到公式:
|
⋃
i
=
1
n
A
i
|
=
∑
i
=
1
n
|
A
i
|
−
∑
1
≤
i
<
j
≤
n
|
A
i
∩
A
j
|
+
∑
1
≤
i
<
j
<
k
≤
n
|
A
i
∩
A
j
∩
A
k
|
−
⋯
+
(
−
1
)
n
−
1
|
A
1
∩
⋯
∩
A
n
|
.
{\displaystyle {\begin{aligned}\left|\bigcup _{i=1}^{n}A_{i}\right|={}&\sum _{i=1}^{n}|A_{i}|-\sum _{1\leq i<j\leq n}|A_{i}\cap A_{j}|+\sum _{1\leq i<j<k\leq n}|A_{i}\cap A_{j}\cap A_{k}|-\cdots +(-1)^{n-1}\left|A_{1}\cap \cdots \cap A_{n}\right|.\end{aligned}}}
又可寫成
|
⋃
i
=
1
n
A
i
|
=
∑
k
=
1
n
(
−
1
)
k
+
1
(
∑
1
≤
i
1
<
⋯
<
i
k
≤
n
|
A
i
1
∩
⋯
∩
A
i
k
|
)
{\displaystyle \left|\bigcup _{i=1}^{n}A_{i}\right|=\sum _{k=1}^{n}(-1)^{k+1}\left(\sum _{1\leq i_{1}<\cdots <i_{k}\leq n}|A_{i_{1}}\cap \cdots \cap A_{i_{k}}|\right)}
或
|
⋃
i
=
1
n
A
i
|
=
∑
∅
≠
J
⊆
{
1
,
2
,
…
,
n
}
(
−
1
)
|
J
|
−
1
|
⋂
j
∈
J
A
j
|
.
{\displaystyle \left|\bigcup _{i=1}^{n}A_{i}\right|=\sum _{\emptyset \neq J\subseteq \{1,2,\ldots ,n\}}(-1)^{|J|-1}{\Biggl |}\bigcap _{j\in J}A_{j}{\Biggr |}.}
在概率論 中,對於概率空間
(
Ω
,
F
,
P
)
{\displaystyle (\Omega ,{\mathcal {F}},\mathbb {P} )}
A 1 ,……,A n n = 2時容斥原理的公式為:
P
(
A
1
∪
A
2
)
=
P
(
A
1
)
+
P
(
A
2
)
−
P
(
A
1
∩
A
2
)
,
{\displaystyle \mathbb {P} (A_{1}\cup A_{2})=\mathbb {P} (A_{1})+\mathbb {P} (A_{2})-\mathbb {P} (A_{1}\cap A_{2}),}
當n = 3時,公式為:
P
(
A
1
∪
A
2
∪
A
3
)
=
P
(
A
1
)
+
P
(
A
2
)
+
P
(
A
3
)
−
P
(
A
1
∩
A
2
)
−
P
(
A
1
∩
A
3
)
−
P
(
A
2
∩
A
3
)
+
P
(
A
1
∩
A
2
∩
A
3
)
{\displaystyle \mathbb {P} (A_{1}\cup A_{2}\cup A_{3})=\mathbb {P} (A_{1})+\mathbb {P} (A_{2})+\mathbb {P} (A_{3})-\mathbb {P} (A_{1}\cap A_{2})-\mathbb {P} (A_{1}\cap A_{3})-\mathbb {P} (A_{2}\cap A_{3})+\mathbb {P} (A_{1}\cap A_{2}\cap A_{3})}
一般地:
P
(
⋃
i
=
1
n
A
i
)
=
∑
i
=
1
n
P
(
A
i
)
−
∑
i
,
j
:
i
<
j
P
(
A
i
∩
A
j
)
+
∑
i
,
j
,
k
:
i
<
j
<
k
P
(
A
i
∩
A
j
∩
A
k
)
−
⋯
+
(
−
1
)
n
−
1
P
(
⋂
i
=
1
n
A
i
)
,
{\displaystyle \mathbb {P} {\biggl (}\bigcup _{i=1}^{n}A_{i}{\biggr )}=\sum _{i=1}^{n}\mathbb {P} (A_{i})-\sum _{i,j\,:\,i<j}\mathbb {P} (A_{i}\cap A_{j})+\sum _{i,j,k\,:\,i<j<k}\mathbb {P} (A_{i}\cap A_{j}\cap A_{k})-\ \cdots \ +(-1)^{n-1}\,\mathbb {P} {\biggl (}\bigcap _{i=1}^{n}A_{i}{\biggr )},}
也可以寫成:
P
(
⋃
i
=
1
n
A
i
)
=
∑
k
=
1
n
(
−
1
)
k
−
1
∑
I
⊂
{
1
,
…
,
n
}
|
I
|
=
k
P
(
A
I
)
,
{\displaystyle \mathbb {P} {\biggl (}\bigcup _{i=1}^{n}A_{i}{\biggr )}=\sum _{k=1}^{n}(-1)^{k-1}\sum _{\scriptstyle I\subset \{1,\ldots ,n\} \atop \scriptstyle |I|=k}\mathbb {P} (A_{I}),}
對於一般的測度空間 (S ,Σ ,μ )和有限測度的可測 子集A 1 ,……,An ,上面的恆等式也成立,如果把概率測度
P
{\displaystyle \mathbb {P} }
μ 。
如果在容斥原理的概率形式中,交集AI 的概率只與I 中元素的個數有關,也就是說,對於{1, ..., n }中的每一個k ,都存在一個ak ,使得:
a
k
=
P
(
A
I
)
{\displaystyle a_{k}=\mathbb {P} (A_{I})}
I
⊂
{
1
,
…
,
n
}
(
|
I
|
=
k
)
,
{\displaystyle I\subset \{1,\ldots ,n\}\,\,(|I|=k),}
則以上的公式可以簡化為:
P
(
⋃
i
=
1
n
A
i
)
=
∑
k
=
1
n
(
−
1
)
k
−
1
(
n
k
)
a
k
{\displaystyle \mathbb {P} {\biggl (}\bigcup _{i=1}^{n}A_{i}{\biggr )}=\sum _{k=1}^{n}(-1)^{k-1}{\binom {n}{k}}a_{k}}
這是由於二項式係數
(
n
k
)
{\displaystyle \scriptstyle {\binom {n}{k}}}
類似地,如果對有限集合A 1 ,……,An 的併集的元素個數感興趣,且對於{1, ..., n }中的每一個k ,交集
A
I
:=
⋂
i
∈
I
A
i
{\displaystyle A_{I}:=\bigcap _{i\in I}A_{i}}
的元素個數都相同,例如ak = |AI |,與{1, ..., n }的k 元素子集I 無關,則:
|
⋃
i
=
1
n
A
i
|
=
∑
k
=
1
n
(
−
1
)
k
−
1
(
n
k
)
a
k
.
{\displaystyle {\biggl |}\bigcup _{i=1}^{n}A_{i}{\biggr |}=\sum _{k=1}^{n}(-1)^{k-1}{\binom {n}{k}}a_{k}\,.}
在一般的測度空間(S ,Σ ,μ )和有限測度的可測子集A 1 ,……,An 的情況中,也可以進行類似的簡化。
欲證明容斥原理,我們首先要驗證以下的關於指示函數 的等式:
1
∪
i
=
1
n
A
i
=
∑
k
=
1
n
(
−
1
)
k
−
1
∑
I
⊂
{
1
,
…
,
n
}
|
I
|
=
k
1
A
I
(
∗
)
{\displaystyle 1_{\cup _{i=1}^{n}A_{i}}=\sum _{k=1}^{n}(-1)^{k-1}\sum _{\scriptstyle I\subset \{1,\ldots ,n\} \atop \scriptstyle |I|=k}1_{A_{I}}\qquad (*)}
至少有兩種方法來證明這個等式:
第一種方法 我們只需證明對於A 1 ,……,An 的併集中的每一個x ,等式都成立。假設x 正好屬於m 個集合(1 ≤ m ≤ n ),不妨設它們為A 1 ,……,Am 。則x 處的等式化為:
1
=
∑
k
=
1
m
(
−
1
)
k
−
1
∑
I
⊂
{
1
,
…
,
m
}
|
I
|
=
k
1.
{\displaystyle 1=\sum _{k=1}^{m}(-1)^{k-1}\sum _{\scriptstyle I\subset \{1,\ldots ,m\} \atop \scriptstyle |I|=k}1.}
m 元素集合中的k 元素子集的個數,是二項式係數
(
m
k
)
{\displaystyle \textstyle {\binom {m}{k}}}
1
=
(
m
0
)
{\displaystyle \textstyle 1={\binom {m}{0}}}
(
m
0
)
=
∑
k
=
1
m
(
−
1
)
k
−
1
(
m
k
)
.
{\displaystyle {\binom {m}{0}}=\sum _{k=1}^{m}(-1)^{k-1}{\binom {m}{k}}.}
把所有的項移到等式的左端,我們便得到(1 – 1)m x 成立。
第二種方法 設A 表示集合A 1 ,……,An 的併集。於是:
0
=
(
1
A
−
1
A
1
)
(
1
A
−
1
A
2
)
⋯
(
1
A
−
1
A
n
)
,
{\displaystyle 0=(1_{A}-1_{A_{1}})(1_{A}-1_{A_{2}})\cdots (1_{A}-1_{A_{n}})\,,}
這是因為對於不在A 內的x ,兩邊都等於零,而如果x 屬於其中一個集合,例如Am ,則對應的第m 個因子為零。把右端的乘積展開來,便可得到等式(*)。
設:S1 = n (A1 )+n (A2 )+n (A3 ) +…...+n (An )
S2 = n(A1 ∩A2 )+ n(A1 ∩A3 ) …...+ n(A1 ∩An )+ n(A2 ∩A3 )+ …...+n(An-1 ∩An)
S3 = n(A1 ∩A2 ∩A3 )+ ……+ n(An-2 ∩An-1 ∩An)……
Sn =n(A1 ∩A2 ∩A3 ∩……∩An )
求證:A=n(A1 ∪A2 ∪A3 ∪A4 ……∪An )= S1 -S2 + S3 +……+(-1)n-1 Sn
證明:當n=2時,A=n(A1 ∪A2 )=n(A1 )+n(A2 ) -n(A1 ∩ A2 )= S1 -S2
假設:當n=k(k>=2)時,A=n (A1 ∪A2 ∪A3 ∪A4 ……∪Ak )= S1 -S2 + S3 +……+(-1)k-1 Sk 等式成立。
當n=k+1時,
A= n( (A1 ∪A2 ∪A3 ∪A4 ……∪Ak ) ∪Ak+1 )
= n (A1 ∪A2 ∪A3 ∪A4 ……∪Ak )+n(Ak+1 )-n((A1 ∪A2 ∪A3 ∪A4 ……∪Ak ) ∩Ak+1 )
= n (A1 ∪A2 ∪A3 ∪A4 ……∪Ak ) +n(Ak+1 )-n((A1 ∩Ak+1 ) ∪(A2 ∩Ak+1 ) ∪(A3 ∩Ak+1 ) ∪ …∪(Ak ∩Ak+1 ))
∵ 當n=k時,等式成立
∴A= n (A1 ∪A2 ∪A3 ∪A4 ……∪Ak ) +n(Ak+1 )-(n (A1 ∩Ak+1 )+ n (A2 ∩Ak+1 )+ ……+n(Ak ∩Ak+1 )-n(A1 ∩A2 ∩Ak+1 )-n(A1 A3 ∩Ak+1 ) -……- n(Ak-1 ∩Ak ∩Ak+1 )+ ……+(-1)k .n(A1 ∩A2 ∩A3 ∩∪……∩Ak+1 )
= S1 -S2 + S3 +……+(-1)k-1 Sk +n(Ak+1 )-(n (A1 ∩Ak+1 )+ n (A2 ∩Ak+1 )+ ……+n(Ak ∩Ak+1 )-n(A1 ∩A2 ∩Ak+1 )-n(A1 ∩A3 ∩Ak+1 ) -……- n(Ak-1 ∩Ak ∩Ak+1 )+ ……+(-1)k .n(A1 ∩A2 ∩A3 ∩∪……∩Ak+1 )
= S1 -S2 + S3 +……+(-1)k Sk+1
綜上所述,當n>=2時,n (A1 ∪A2 ∪A3 ∪A4 ……∪An )
= n (A1 )+n (A2 )+n (A3 ) ……+ n (An )-n(A1 ∩A2 )- n(A1 ∩A3 ) ……- n(A1 ∩An )- n(A2 ∩A3 )- ……-n(An-1 ∩An)+n(A1 ∩A2 ∩A3 )+ n(A1 ∩A2 ∩A3 )+ ……+ n(An-2 ∩An-1 ∩An)- ……+……+(-1)n-1 .n(A1 ∩A2 ∩A3 ∩……∩An )[ 1]
有時容斥原理用以下的形式來表述:如果
g
(
A
)
=
∑
S
:
S
⊆
A
f
(
S
)
{\displaystyle g(A)=\sum _{S\,:\,S\subseteq A}f(S)}
那麼:
f
(
A
)
=
∑
S
:
S
⊆
A
(
−
1
)
|
A
|
−
|
S
|
g
(
S
)
{\displaystyle f(A)=\sum _{S\,:\,S\subseteq A}(-1)^{\left|A\right|-\left|S\right|}g(S)}
在這種形式中可以看出,它是A 的所有子集的偏序集合 的指標代數 的莫比烏斯反演公式 。
在許多情況下,容斥原理都可以給出精確的公式(特別是用埃拉托斯特尼篩法 計算素數 的個數時),但是用處不大,這是因為它裡面含有的項太多。即使每一個單獨的項都可以準確地估計,誤差累積起來仍然意味着容斥原理不能直接應用。在數論 中,這個困難由維戈·布朗 解決。開始時進展很慢,但他的想法逐漸被其他數學家所應用,於是便產生了許多各種各樣的篩法 。這些方法是嘗試找出被「篩選」的集合的上界,而不是一個確切的公式。
容斥原理的一個著名的應用,是計算一個有限集合的所有亂序 排列的數目。一個集合A 的錯排 ,是從A 到A 的沒有不動點的雙射 。通過容斥原理,我們可以證明,如果A 含有n 個元素,則亂序排列的數目為[n ! / e ],其中[x ]表示最接近x 的整數。
這也稱為n 的子階乘 ,記為!n 。可以推出,如果所有的雙射都有相同的概率,則當n 增大時,一個隨機雙射是錯排的概率迅速趨近於1/e 。
容斥原理與德·摩根定理 結合起來,也可以用於計算集合的交集中元素的數目。設
A
¯
k
{\displaystyle \scriptstyle {\overline {A}}_{k}}
A k A 的補集 ,使得對於每一個k ,都有
A
k
⊆
A
{\displaystyle \scriptstyle A_{k}\,\subseteq \,A}
⋂
i
=
1
n
A
i
=
⋃
i
=
1
n
A
¯
i
¯
{\displaystyle \bigcap _{i=1}^{n}A_{i}={\overline {\bigcup _{i=1}^{n}{\overline {A}}_{i}}}}
這樣便把計算交集的問題化為計算併集的問題。