在數學中,給定兩個群 和
和 ,從
,從  到
到  的群同態(Group homomorphism)是函數
的群同態(Group homomorphism)是函數 使得對於所有
使得對於所有 中的
中的 和
和 下述等式成立
下述等式成立
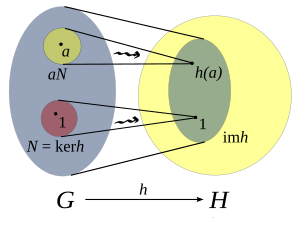 從
從 (左)到
(左)到 (右)的群同態(
(右)的群同態( )的像。在
)的像。在 內的橢圓形是
內的橢圓形是 的像。
的像。 是
是 的核而
的核而 是
是 的陪集。
的陪集。

在這裏,等號左側的群運算 ,是
,是 中的運算;而右側的運算
中的運算;而右側的運算 是
是 中的運算。
中的運算。
從這個性質,可推導出 將
將 的單位元
的單位元 映射到
映射到 的單位元
的單位元 ,並且它還在
,並且它還在 的意義上映射反元素到反元素。因此我們可以說
的意義上映射反元素到反元素。因此我們可以說 「兼容於群結構」。
「兼容於群結構」。
過去同態 常用
常用 或
或 來表示,它容易混淆於索引或一般下標。更新近的傾向是把群同態寫在它們的自變量的右側,省略括號,如此
來表示,它容易混淆於索引或一般下標。更新近的傾向是把群同態寫在它們的自變量的右側,省略括號,如此 簡化成了
簡化成了 。這種方法因為其更適應自動機從左至右讀字的習慣從而在某些廣泛應用自動機理論的群論中頗為流行。
。這種方法因為其更適應自動機從左至右讀字的習慣從而在某些廣泛應用自動機理論的群論中頗為流行。
在考慮有額外的結構的群的數學領域中,同態不僅要滿足上述的群結構,還要滿足額外的結構。比如拓撲群的同態經常要求是連續的。
- 考慮帶有加法的循環群 和整數集 的群。映射 ,有 為 模以3,是群同態。它是滿射並且它的核由被三整除的所有整數構成。
- 指數映射產生從帶有加法的實數集 的群到帶有乘法的非零實數集 的群的群同態。核是 而像由正實數組成。
- 指數映射還產生從帶有加法的複數集 的群到帶有乘法的非零複數集 的群的同態。這個映射是滿射並且有核 ,這可以從歐拉公式得出。
- 給定任何兩個群 和 ,映射 ,把所有 的元素對應到 的單位元,是同態;它的核是集合 。
- 給定任何群 ,恆等映射 定義為對於 中所有的 , 。恆等映射是群同態。
- Lang, Serge, Algebra, Graduate Texts in Mathematics 211 3rd, Springer-Verlag, 2002 .





















