五複合立方體
在幾何學中,五複合立方體,是一種由五個立方體組合成的複合多面體,其索引編號為UC9,是唯一五種正複合體之一[3],亦是一種星形多面體。埃德蒙·赫斯在1876年首先描述了該幾何結構。
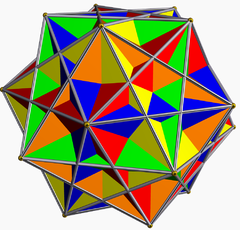 五複合立方體,每個立方體以不同顏色表示 | ||||||||||||
| 類別 | 複合正多面體 星形菱形三十面體 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 對偶多面體 | 五複合正八面體 | |||||||||||
| 識別 | ||||||||||||
| 名稱 | 五複合立方體 | |||||||||||
| 參考索引 | UC5 | |||||||||||
| 數學表示法 | ||||||||||||
| 考克斯特符號 | 2{5,3}[5{4,3}][2] | |||||||||||
| 性質 | ||||||||||||
| 體 | 5 | |||||||||||
| 面 | 30 | |||||||||||
| 邊 | 60 | |||||||||||
| 頂點 | 20 | |||||||||||
| 歐拉特徵數 | F=30, E=60, V=20 (χ=-10) | |||||||||||
| 組成與佈局 | ||||||||||||
| 複合幾何體數量 | 5 | |||||||||||
| 複合幾何體種類 | 5個立方體 | |||||||||||
| 面的種類 | 30個正方形 | |||||||||||
| 對稱性 | ||||||||||||
| 對稱群 | 二十面體群 (Ih) | |||||||||||
| 圖像 | ||||||||||||
| ||||||||||||
構造
編輯擁有二十面體對稱五複合立方體可以由以原點為中心、面向軸的第一個立方體開始構造,其餘的立方體則透過軸 旋轉 弧度來構造,畢依這加入順序決定角度值中的n,例如第二個立方體n=1、第三個立方體n=2以此類推。
性質
編輯五複合立方體為五個立方體組合成的形狀,因此其邊、面和頂點的數量基本上應該會是立方體的5倍,但因為部分頂點是重合的,因此其僅有30個面、60條邊和20個頂點。
五複合立方體中可以找到菱形三十面體中的30個菱形[4][5]。
結構
編輯五複合立方體可以視為正十二面體刻面後的多面體,在正十二面體凸包中每個立方體定位在12個頂點中的其中8個頂點。
| |
頂點座標
編輯由於五複合立方體可以看作是在正十二面體中嵌入立方體,因此其頂點座標與正十二面體相同:
- (±1, ±1, ±1)
- (0, ±1/ϕ, ±ϕ)
- (±1/ϕ, ±ϕ, 0)
- (±ϕ, 0, ±1/ϕ)
其中ϕ = 1 + √5/2為黃金比例。
作為星形多面體
編輯五複合立方體可以看作是一種菱形三十面體的星形多面體,即星形菱形三十面體[6][7]。
| 星狀圖 | 星形 | 星狀核 | 凸包 |
|---|---|---|---|
| 菱形三十面體 |
正十二面體 |
稜排佈
編輯五複合立方體的凸包是正十二面體。其與一些凸包也是正十二面體的多面體有着相同的稜排佈,例如小雙三斜三十二面體、大雙三斜三十二面體和雙三斜十二面體。
| a{5,3} | a{5/2,3} | b{5,5/2} |
|---|---|---|
| = | = | |
| 小雙三斜三十二面體 |
大雙三斜三十二面體 |
雙三斜十二面體 |
| 正十二面體 (凸包) |
五複合立方體 |
球面的五複合立方體 |
其他的五個立方體複合圖形
編輯亦有其他也由五個立方體組合成的形狀,例如佛達里也斯的五複合立方體。這種形狀是一個八面體對稱的星形多面體。
參考文獻
編輯- Cromwell, Peter R., Polyhedra, Cambridge, 1997. p 360
- Harman, Michael G., Polyhedral Compounds, unpublished manuscript, c. 1974 [2016-09-01], (原始內容存檔於2013-07-31).
- Skilling, John, Uniform Compounds of Uniform Polyhedra, Mathematical Proceedings of the Cambridge Philosophical Society, 1976, 79: 447–457, MR 0397554, doi:10.1017/S0305004100052440.
- Cundy, H. and Rollett, A. "Five Cubes in a Dodecahedron." §3.10.6 in Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., pp. 135–136, 1989.
- ^ 1.0 1.1 H.S.M. Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8
- ^ Regular Polytopes (1973)[1] pp.49-50, p.98
- ^ Regular Polytopes (1973)[1], 3.6 The five regular compounds, pp.47-50
- ^ Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, 1999. ISBN 978-0486409146 p. 199
- ^ Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 135 and 137, 1987. ISBN 978-0486253572
- ^ Weisstein, Eric W. (編). Compound of Five Cubes. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英語).
- ^ Kabai, S. Mathematical Graphics I: Lessons in Computer Graphics Using Mathematica. Püspökladány, Hungary: Uniconstant, pp. 161 and 185, 2002.