折線
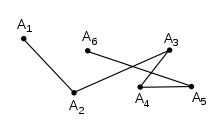
折線又稱多邊形鏈(polygonal chain)[註 1]或多段線(polyline)[5]是指一系列相連的線段,通常是一些任意不同方向的直線段首尾相連結所形成的線[7]。 與多邊形不同,折線並不要求線的整體要頭尾封閉。 更正式地說,折線P是由一系列稱為其頂點的點所決定的曲線,該曲線連續地由線段連接這些頂點所構成。


變體
編輯簡單折線
編輯簡單折線是指該折線的線段連續相交,且僅有在線段的端點相交,沒有在別處有相交(即非自相交的折線)。
封閉折線
編輯封閉折線是指第一個頂點與最後一個頂點重合,或者第一個頂點與最後一個頂點也相連的折線。[8] 平面的簡單封閉折線是簡單多邊形的邊界。 通常,「多邊形」這個術語就是指「封閉折線」,但在某些情況下還是會將封閉折線和多邊形兩個概念區分開來。
單調折線
編輯如果存在一條直線L,且垂直於L的每條直線最多與該折線相交一次,則稱該折線是一個單調折線。每個非平凡的單調多邊形鏈都是非封閉的(開放的)。 相較之下,每個單調多邊形(封閉折線)都恰好可以分割成兩個單調折線。[9] 分段線性函數的圖形相對於水平線形成單調折線。 一般的折線圖也都是相對於某座標軸的單調折線。
參數化
編輯折線的每個線段通常使用連續頂點間的線性插值來線性參數化。 在實際應用中,對於整條折線而言有兩種常見的參數化方式。 一種是:折線之線段鏈的每一段都可以被分配與第一個頂點對應索引的參數之單位區間; 另一種是:折線之線段鏈的每一段都可以被分配一個與該段的長度相對應的參數區間,使得該參數沿着整個折線之線段鏈統一對應於其曲線長。
與點集的關聯
編輯每個至少有n個點的點集都包含一條至少有 條邊的斜率正負相同之折線路徑。 這是埃爾多斯-塞克雷斯定理的推論。
應用
編輯折線通常可以用來近似更複雜的曲線。 在這種情況下,道格拉斯-普克演算法可以用於尋找具有最少線段但又足夠接近原始曲線的折線,作為該曲線精確的近似。[10][11]
在圖繪製中,折線常用於表示圖的邊,在繪圖樣式中,將邊繪製為直線段可能會導致交叉、邊與頂點碰撞或其他不希望出現的特徵。 在這種情況下,通常希望用盡可能少的線段和彎曲來繪製圖的邊,以減少繪圖中的視覺混亂; 最小化彎曲次數的問題稱為彎曲最小化問題。[12]
折線也是計算幾何的一種基本資料類型。 例如,李德財和普雷帕拉塔的點定位演算法就是透過將任意曲面細分分解為單調折線的有序序列來進行操作,以達到可以透過二分搜尋來解決點位置查詢問題的目標; 此方法後來經過改進,使得點定位問題的時間複雜度得到最佳化。[13]
參見
編輯註釋
編輯參考文獻
編輯- ^ Gomes, Jonas; Velho, Luiz; Costa Sousa, Mario, Computer Graphics: Theory and Practice, CRC Press: 186, 2012, ISBN 9781568815800.
- ^ Cheney, Ward, Analysis for Applied Mathematics, Graduate Texts in Mathematics 208, Springer: 13, 2001, ISBN 9780387952796.
- ^ 3.0 3.1 Boissonnat, Jean-Daniel; Teillaud, Monique, Effective Computational Geometry for Curves and Surfaces, Springer: 34, 2006, ISBN 9783540332596.
- ^ Muggeo, Vito M. R., segmented: An R package to fit regression models with broken-line relationships (PDF), R News, May 2008, 8 (1): 20–25
- ^ 5.0 5.1 折線 polyline. 雙語詞彙、學術名詞暨辭書資訊網. 國家教育研究院. [2023-12-03]. (原始內容存檔於2023-12-03).
- ^ Open Geospatial Consortium, Herring, John R. , 編, OpenGIS® Implementation Standard for Geographic information - Simple feature access - Part 1: Common architecture, 1.2.1, Open Geospatial Consortium, 2011-05-28 [2016-01-15], (原始內容存檔於2017-01-29)
- ^ 折線. 教育部重編國語辭典. [2023-11-17]. (原始內容存檔於2023-11-17).
- ^ Mehlhorn, Kurt; Näher, Stefan, LEDA: A Platform for Combinatorial and Geometric Computing, Cambridge University Press: 758, 1999, ISBN 9780521563291.
- ^ O'Rourke, Joseph, Computational Geometry in C, Cambridge Tracts in Theoretical Computer Science, Cambridge University Press: 45, 1998, ISBN 9780521649766.
- ^ Ramer, Urs, An iterative procedure for the polygonal approximation of plane curves, Computer Graphics and Image Processing, 1972, 1 (3): 244–256, doi:10.1016/S0146-664X(72)80017-0.
- ^ Douglas, David; Peucker, Thomas, Algorithms for the reduction of the number of points required to represent a digitized line or its caricature, The Canadian Cartographer, 1973, 10 (2): 112–122, doi:10.3138/FM57-6770-U75U-7727.
- ^ Tamassia, Roberto, On embedding a graph in the grid with the minimum number of bends, SIAM Journal on Computing, 1987, 16 (3): 421–444, doi:10.1137/0216030.
- ^ Edelsbrunner, Herbert; Guibas, Leonidas J.; Stolfi, Jorge, Optimal point location in a monotone subdivision, SIAM Journal on Computing, 1986, 15 (2): 317–340, doi:10.1137/0215023.
