星形线

星形线（astroid）或称为四尖瓣线（tetracuspid），是一个有四个尖点的内摆线，也属于超椭圆的一种。所有星形线皆可以依以下的方程式比例缩放而得^[1]：

x^{2/3}+y^{2/3}=a^{2/3}.\,

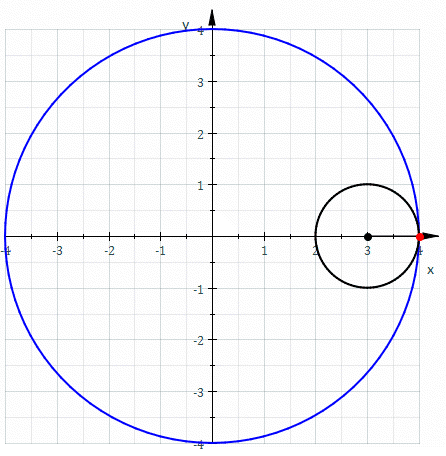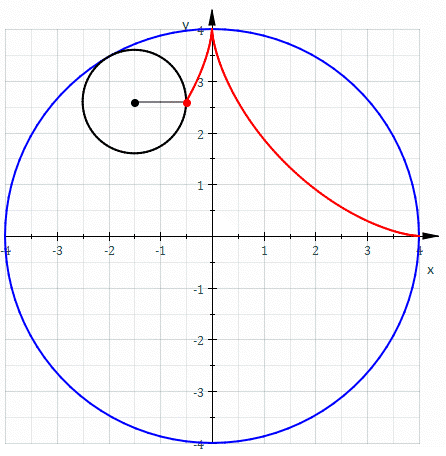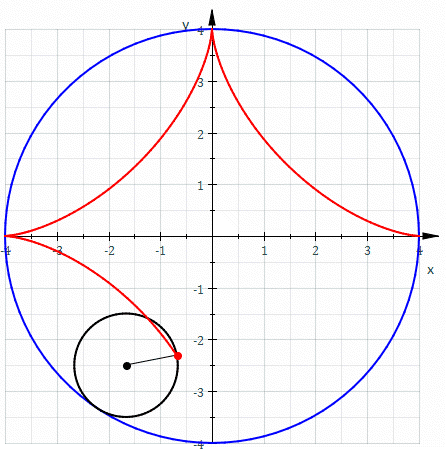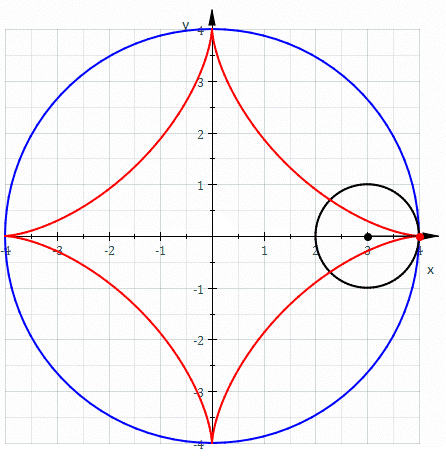
其英文名称得名自希腊文的“星星”，星形线几乎和椭圆的渐屈线相同。

若让一个半径为1/4的圆在一个半径为1的圆内部，延著圆的圆周旋转，小圆圆周上的任一点形成的轨迹即为星形线。星形线的参数方程为^[1]：

x=a\cos ^{3}\theta ,\qquad y=a\sin ^{3}\theta .

星形线是一个几何亏格（英语：geometric genus）为0代数曲线的实数轨迹，其方程式如下：

(x^{2}+y^{2}-1)^{3}+27x^{2}y^{2}=0.\,

因此星形线为六次曲线，在实数平面上有四个尖瓣的奇点，分别是星形线的四个顶点，在无限远处还有二个复数的尖瓣的奇点，四个重根的复数奇点，因此星形线共有十个奇点。

星形线的对偶曲线（英语：Dual curve）是十字架形曲线（英语：cruciform curve），其方程式为 $\textstyle x^{2}y^{2}=x^{2}+y^{2}.$ 。星形线的渐屈线为另一个二倍大的渐屈线。

一个半径为 $a$ 之圆的内摆线构成的星形线，其面积为 ${\frac {3}{8}}\pi a^{2}$ ，周长为6a。

参考资料

^ ^1.0 ^1.1 清华大学数学科学系. 微积分. 北京: 清华大学出版社有限公司. 2003: 47–48 [2012-12-21]. ISBN 7302067856. （原始内容存档于2019-05-28）.

J. Dennis Lawrence. A catalog of special plane curves. Dover Publications. 1972: 4–5,34–35,173–174. ISBN 0-486-60288-5.
Wells D. The Penguin Dictionary of Curious and Interesting Geometry. New York: Penguin Books. 1991: 10–11. ISBN 0-14-011813-6.
R.C. Yates. Astroid. A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards. 1952: 1 ff.