半正多面體

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
|

|

|

|
半正多面體是泛指所有由超過一種正多邊形所組成的多面體,並且要有對稱群,根據托羅爾德戈塞特的1900定義半正多面體[1][2]有下面幾種:
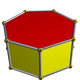
半正多面體並非只包含阿基米德立體[3][4],它包含了所有由正多邊形組成且具有嚴格對稱的多面體,包含了正稜柱和正反稜柱
這些半正多面體可以完全由一種頂點配置來描述。例如:3.5.3.5,表示截半二十面體,即每個頂點周圍都有2個三角形和2個五邊形。而若頂點配置有些微差異就會變成另外一種半正多面體,像是3.3.3.5是一個五角反稜柱。這些多面體有時被描述為vertex-transitive。
從Gosset開始有其他作者使用術語「半正」,以不同的方式,描述更高維度的立體。E. L. Elte[5]提供了一種被考克斯特認為過於太人為的定義。考克斯特自己冠以戈塞特的數據正圖形,但只有相當有限的子集分類為半正圖形[6]。
然而,其他人採取了不同的方式,來分類半正多面體。這些內容包括:
進一步引起爭議的根源在於,阿基米德多面體的定義再次出現不同的解釋方式。
Gosset定義的半正多面體有更高的對稱性,正多面體和擬正多面體,後來的一些學者認為,這些都不是半正多面體,因為他們過於「正」了,並認為均勻多面體比較適合,這個命名系統的比較好,並協調許多(但絕不是全部)爭議。
參考文獻
編輯- ^ Thorold Gosset On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
- ^ Coxeter, H.S.M. Regular polytopes, 3rd Edn, Dover (1973)
- ^ 《圖解數學辭典》天下遠見出版 ISBN 986-417-614-5
- ^ Illustrated Dictionary of Maths 2003 Usborne Publishing Ltd.
- ^ Elte, E. L., The Semiregular Polytopes of the Hyperspaces, Groningen: University of Groningen, 1912
- ^ Coxeter, H.S.M., Longuet-Higgins, M.S. and Miller, J.C.P. Uniform Polyhedra, Philosophical Transactions of the Royal Society of London 246 A (1954), pp. 401-450. (JSTOR archive, subscription required).
- 埃里克·韋斯坦因. Semiregular polyhedron. MathWorld.
- George Hart: Archimedean Semi-regular Polyhedra(頁面存檔備份,存於網際網路檔案館)
- David Darling: semi-regular polyhedron
- polyhedra.mathmos.net: Semi-Regular Polyhedron(頁面存檔備份,存於網際網路檔案館)
- Encyclopaedia of Mathematics: Semi-regular polyhedra, uniform polyhedra, Archimedean solids(頁面存檔備份,存於網際網路檔案館)