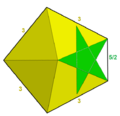
扭稜大星形十二面體

扭稜大星形十二面體是一種星形均勻多面體，為大星形十二面體經過扭稜變換後的像，由80個正三角形和12個正五角星組成，索引為U₅₇，對偶多面體為大五角六十面體，具有二十面體群對稱性。

扭稜大星形十二面體

類別	均勻星形多面體
對偶多面體	大五角六十面體
識別
名稱	扭稜大星形十二面體 great snub icosidodecahedron
參考索引	U57, C88, W113
鮑爾斯縮寫	gosid
數學表示法
考克斯特符號
施萊夫利符號	sr{5⁄2,3}
威佐夫符號	| 2 5/2 3
性質
面	92
邊	150
頂點	60
歐拉特徵數	F=92, E=150, V=60 （χ=2）
組成與佈局
面的種類	(20+60)個正三角形 12個正五角星
頂點圖	3.3.3.3.5⁄2
對稱性
對稱群	Ih, [5,3]+, 532
圖像
3.3.3.3.5⁄2 （頂點圖） 大五角六十面體 （對偶多面體）

性質

扭稜大星形十二面體共由92個面、150條邊和60個頂點組成。在其92個面中有80個正三角形面和12個五角星面，這80個三角形面中有60個來自扭稜變換。在其60個頂點中，每個頂點都是4個正三角形面和1個正五角星面的公共頂點，並且這些面在構成頂角的多面角時，以正五角星、正三角形、正三角形、正三角形和正三角形的順序排列，在頂點圖中可以用(5/2.3.3.3.3)來表示。

表示法

扭稜大星形十二面體在考克斯特—迪肯符號中可以表示為，在施萊夫利符號中可以表示為sr{5⁄2,3}，在威佐夫記號中可以表示為| 2 5/2 3。

尺寸

若扭稜大星形十二面體的邊長為單位長，則其外接球半徑為：

$R={\frac {1}{2}}{\sqrt {\frac {2-x}{1-x}}}=0.64502\dots$

其中$x$是$x^{3}+2x^{2}={\Big (}{\tfrac {1\pm {\sqrt {5}}}{2}}{\Big )}^{2}$的實根。 以$R^{2}$為變數的六次方程式

$4096R^{12}-27648R^{10}+47104R^{8}-35776R^{6}+13872R^{4}-2696R^{2}+209=0$

共有4個實根，分別是扭棱十二面體、扭稜大星形十二面體、反扭稜大星形十二面體和大反屈扭稜截半二十面體的外接球半徑。

頂點座標

扭稜大星形十二面體的頂點座標為下列座標的偶置換：

$\left(\pm 2\alpha ,\pm 2,\pm 2\beta \right)$、

$\left(\pm \left(\alpha -\beta \tau -{\frac {1}{\tau }}\right),\pm \left({\frac {\alpha }{\tau }}+\beta -\tau \right),\pm \left(-\alpha \tau -{\frac {\beta }{\tau }}-1\right)\right)$、

$\left(\pm \left(\alpha \tau -{\frac {\beta }{\tau }}+1\right),\pm \left(-\alpha -\beta \tau +{\frac {1}{\tau }}\right),\pm \left(-{\frac {\alpha }{\tau }}+\beta +\tau \right)\right)$、

$\left(\pm \left(\alpha \tau -{\frac {\beta }{\tau }}-1\right),\pm \left(\alpha +\beta \tau +{\frac {1}{\tau }}\right),\pm \left(-{\frac {\alpha }{\tau }}+\beta -\tau \right)\right)$和

$\left(\pm \left(\alpha -\beta \tau +{\frac {1}{\tau }}\right),\pm \left(-{\frac {\alpha }{\tau }}-\beta -\tau \right),\pm \left(-\alpha \tau -{\frac {\beta }{\tau }}+1\right)\right)$，

帶有偶數個正號，其中

$\alpha ={\frac {\xi -1}{\xi }}$

且

$\beta =-{\frac {\xi }{\tau }}+{\frac {1}{\tau ^{2}}}-{\frac {1}{\xi \tau }}$

其中$\tau ={\frac {1+{\sqrt {5}}}{2}}$為黃金比例、 $\xi$是方程式$\xi ^{3}-2\xi =-{\frac {1}{\tau }}$的負實根，約為−1.5488772。 若上述座標使用奇置換並帶有奇數個正號的話，則會得到扭稜大星形十二面體的另一種形式，即另一種形式的手性對映體。

參見

• 均勻多面體列表
• 反扭稜大星形十二面體