錐台

稜台是幾何學中研究的一類多面體，指一個稜錐被平行於它的底面的一個平面所截後，截面與底面之間的幾何形體。截面也稱為稜台的上底面，原來稜錐的底面稱為下底面。隨著稜錐形狀不同，稜台的稱呼也不相同，依底面多邊形而定，例如底面是正方形的稜台稱為方稜台，底面為三角形的稜台稱為三稜台，底面為五邊形的稜台稱為五稜台等等。稜台是平截頭體的一類，也是更廣義的擬柱體的一種。根據所截的是圓錐還是稜錐，可分為圓台與稜台。

錐台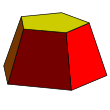

例如：五角錐台與四角錐台
類別	錐台
對偶多面體	不對稱雙錐體
性質
面	${{n}+{2}}$
邊	${{3}\,{n}}$
頂點	${{2}\,{n}}$
歐拉特徵數	F=${{n}+{2}}$, E=${{3}\,{n}}$, V=${{2}\,{n}}$ （χ=2）
組成與佈局
面的種類	n 個梯形, 2 個n邊形
對稱性
對稱群	Cnv, [1,n], (*nn)
特性
凸多面體
圖像
不對稱雙錐體 （對偶多面體） （展開圖）
註：$n$為底面邊數 。

從稜台的定義可以推知，一個以n邊形為底面的稜台，一共有2n個頂點，n+2個面以及3n條邊。稜台的對偶多面體是雙錐。稜台的對稱性取決於原來稜錐。如果原來的稜錐是正稜錐，那麼稜台和正多邊形有相同的對稱結構（同構的對稱群）。

性質

體積

稜台的體積取決於兩底面之間的距離（稜台的高），以及原來稜錐的體積。設$h$為稜台的高，$S_{u}$和$S_{d}$為稜台的上下底面積，$V$ 為稜台的體積。由於稜台是由一個平面截去稜錐的一部分（也就是和原來稜錐相似的一個小稜錐）得到，所以計算體積的時候，可以先算出原來稜錐的體積，再減去和它相似的小稜錐的體積。稜錐被平行於底面的平面所截時，截面的面積與底面面積的比，等於小稜錐和原稜錐的高的比的平方。假設原稜錐的高是$H$，那麼小稜錐的高是$H-h$。也就是說：

${\frac {H-h}{H}}={\sqrt {\frac {S_{u}}{S_{d}}}}$

所以：

$H={\frac {h{\sqrt {S_{d}}}}{{\sqrt {S_{d}}}-{\sqrt {S_{u}}}}}$

稜台的體積等於原稜錐體積減去小稜錐的體積：

$V={\frac {S_{d}H}{3}}-{\frac {S_{u}(H-h)}{3}}={\frac {(S_{d}{\sqrt {S_{d}}}-S_{u}{\sqrt {S_{u}}})h}{3({\sqrt {S_{d}}}-{\sqrt {S_{u}}})}}={\frac {h}{3}}\left(S_{d}+S_{u}+{\sqrt {S_{d}}}{\sqrt {S_{u}}}\right)$

對於正稜錐，假設它的底面是正n邊形，邊長分別為a和b，高是h，那麼底面積是：$S_{u}={\frac {na^{2}}{4}}\cot {\frac {\pi }{n}},\quad S_{u}={\frac {nb^{2}}{4}}\cot {\frac {\pi }{n}}.$ 所以它的體積是：

$V={\frac {n(a^{2}+b^{2}+ab)h}{12}}\cot {\frac {\pi }{n}}.$

表面積

稜台的側面展開圖是由各個梯形側面組成的，展開圖的面積，就是各個側面的面積之和，也就是原稜錐的側面積減去小稜錐的側面積S_c

$S_{c}=\sum _{i=1}^{n}S_{i}$，其中$S_{i},i=1,2\cdots ,n$是第 i 個側面的面積。

稜台的表面積等於稜台的側面積S_c加上底面積S。假設各個梯形側面的高是h_i，底邊的長度是a_i和b_i，那麼稜錐的側面積：

$S_{c}=\sum _{i=1}^{n}S_{i}={\frac {1}{2}}\sum _{i=1}^{n}(a_{i}+b_{i})h_{i}.$

體積公式

稜台或圓台的體積是原立體圖形的體積減去被截去部分的體積：

$V={\frac {h_{2}B_{2}-h_{1}B_{1}}{3}}$

B₁ 指一個底面的面積，B₂指另一個底面的面積, and h₁， h₂ 指原頂點分別到兩底面的面積。 考慮到

${\frac {B_{1}}{h_{1}^{2}}}={\frac {B_{2}}{h_{2}^{2}}}$

這個體積也可用平截頭體的高 h = h₂−h₁ 與兩底面面積的希羅平均數表達：

$V={\frac {h}{3}}(B_{1}+B_{2}+{\sqrt {B_{1}B_{2}}})$

亞歷山大里亞的希羅 推導出了這個公式並且憑藉它遇到了虛數。

特別地， 圓台的體積是

$V={\frac {\pi h}{3}}(R_{1}^{2}+R_{2}^{2}+R_{1}R_{2})$

π 等於 3.14159265...，'R₁, R₂ 是兩底面的半徑。

Pyramidal frustum.

底面為n邊形的稜台的體積是

$V={\frac {nh}{12}}(a_{1}^{2}+a_{2}^{2}+a_{1}a_{2})\cot {\frac {180}{n}}$

a₁ 與 a₂ 是底面的邊長。

表面積公式

對於一個正圓台，

${\begin{aligned}{\text{Lateral Surface Area}}&=\pi (R_{1}+R_{2})s\\&=\pi (R_{1}+R_{2}){\sqrt {(R_{1}-R_{2})^{2}+h^{2}}}\end{aligned}}$

${\begin{aligned}{\text{Total Surface Area}}&=\pi \left[(R_{1}+R_{2})s+R_{1}^{2}+R_{2}^{2}\right]\\&=\pi \left[(R_{1}+R_{2}){\sqrt {(R_{1}-R_{2})^{2}+h^{2}}}+R_{1}^{2}+R_{2}^{2}\right]\end{aligned}}$

Lateral Surface Area指側面積，Total Surface Area指總面積，R₁ and R₂ 為底面半徑，s 為平截頭體的斜高。 一個底面為正n邊形的正稜台的表面積是

$A={\frac {n}{4}}\left[(a_{1}^{2}+a_{2}^{2})\cot {\frac {\pi }{n}}+{\sqrt {(a_{1}^{2}-a_{2}^{2})^{2}\sec ^{2}{\frac {\pi }{n}}+4h^{2}(a_{1}+a_{2})^{2}}}\right]$

a₁ 與 a₂是兩底面的邊長。

參見

• 金字塔：某些金字塔是稜台狀建築，大部分是四稜台；
• 圓台：平行於圓錐底面的平面截圓錐，截面和底面之間的部分；
• 稜錐：多邊形的各個頂點與平面外一點相連得到的幾何體。
• 雙錐台
• 錐體

連結

• Derivation of formula for the volume of frustums of pyramid and cone (Mathalino.com)
• 埃里克·韋斯坦因. Pyramidal frustum. MathWorld. 
• 埃里克·韋斯坦因. Conical frustum. MathWorld. 
• Paper models of frustums (truncated pyramids) （頁面存檔備份，存於網際網路檔案館）
• Paper model of frustum (truncated cone) （頁面存檔備份，存於網際網路檔案館）
• Design paper models of conical frustum (truncated cones) （頁面存檔備份，存於網際網路檔案館）