完全圖
在图论中,完全图是一个简单的无向图,其中每一对不同的顶点都只有一条边相连。完全有向图是一个有向图,其中每一对不同的顶点都只有一对边相连(每个方向各一个)。
| 完全图 | |
|---|---|
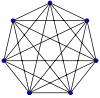 K7,含有7个顶点的完全图 | |
| 顶点 | n |
| 边 | |
| 自同构群 | n!(Sn) |
| 色数 | n
|
| 属性 | (n-1)-正则 顶点传递 边传递 单位距离 强正则 |
图论起源于欧拉在1736年解决七桥问题上做的工作,但是通过将顶点放在正多边形上来绘制完全图的尝试,早在13世纪拉蒙·柳利 的工作中就出现了[1]。这种画法有时被称作神秘玫瑰。
性质
编辑在 个顶点上的完全图被记作 ,有些文献认为这个记号中的字母 代表德文 komplett,[2] 但是完全图的德文vollständiger Graph,并没有字母 ,其他文献认为这个记号是为了纪念卡齐米日·库拉托夫斯基对图论的贡献。[3]
有 条边,并且是 正则图。所有的完全图都是它们本身的极大团。它们是极大连通的,因为唯一的割点集(vertex cut)是所有顶点的集合。完全图的补图是空图(empty graph)。
完全图的每一条边都被附上了定向之后形成的有向图被称作轮转(tournament)。
可以被分解成 个树 ,且 有 个顶点。[4] Ringel猜想可以被表述为:完全图 能否被分解成一些完全相同的 阶树。[5] 对于足够大的 ,这个结论是成立的。[6][7]
完全图的匹配数按照它们的阶数排列,由telephone numbers给出: 1, 1, 2, 4, 10, 26, 76, 232, 764, 2620, 9496, 35696, 140152, 568504, 2390480, 10349536, 46206736, ... (OEIS數列A000085)。这些数字给出了在 阶图上Hosoya指数的最大可能值。[8] 在 上的完美匹配(perfect matching)的个数为 !!。 对于阶数小于等于27阶的完全图来说,它们的交叉数是已知的, 的交叉数是7233或者7234。阶数更大的交叉数由Rectilinear Crossing Number project在收集。[9] 的Rectilinear交叉数为:0, 0, 0, 0, 1, 3, 9, 19, 36, 62, 102, 153, 229, 324, 447, 603, 798, 1029, 1318, 1657, 2055, 2528, 3077, 3699, 4430, 5250, 6180, ... (OEIS數列A014540)。
几何和拓扑
编辑阶完全图可以代表 -单纯形。几何上, 构成了三角形, 构成了四面体,依次类推。Császár polyhedron, 一个非凸的和环面同胚的多边形,可以由 作为它的骨架skeleton。
到 都是平面图,然而当 时,在平面上绘制 时总是会有交叉,另外,非平面图 在刻画平面图的性质时起着重要的作用:根据Kuratowski's theorem,当且仅当一个图不包含 ,以及完全二分图 作为它的一部分时,这个图是平面图。根据Wagner's theorem,当且仅当一个图不包含 ,以及完全二分图 作为它的图子式时,这个图是平面图。 作为Petersen family的一部分, 起到了一个了类似的作用,为了保证一个图的linkless embedding,它不能作为这个图的图子式出现。[10] 更精确地说,Conway和Gordon[11] 证明了每一个 在3维空间中的嵌入都是intrinsically linked 的,且至少有一对linked的三角形。Conway和Gordon还证明了 任意 在3维空间中的嵌入都包含了一个作为一个非平凡的扭结嵌入在空间里的哈密顿环。
例子
编辑| K1: 0 | K2: 1 | K3: 3 | K4: 6 |
|---|---|---|---|
| K5: 10 | K6: 15 | K7: 21 | K8: 28 |
| K9: 36 | K10: 45 | K11: 55 | K12: 66 |
另见
编辑- Fully connected network:全连接网络
- 完全二分图,一种特殊的二分图,其中每个节点都和另一个部分的所有节点相连。
参考文献
编辑- ^ Knuth, Donald E., Two thousand years of combinatorics, Wilson, Robin; Watkins, John J. (编), Combinatorics: Ancient and Modern, Oxford University Press: 7–37, 2013 [2020-10-04], ISBN 978-0191630620, (原始内容存档于2020-07-29).
- ^ Gries, David; Schneider, Fred B., A Logical Approach to Discrete Math, Springer-Verlag: 436, 1993 [2020-10-04], ISBN 0387941150, (原始内容存档于2014-01-02).
- ^ Pirnot, Thomas L., Mathematics All Around, Addison Wesley: 154, 2000, ISBN 9780201308150.
- ^ Joos, Felix; Kim, Jaehoon; Kühn, Daniela; Osthus, Deryk. Optimal packings of bounded degree trees (PDF). Journal of the European Mathematical Society. 2019-08-05, 21 (12): 3573–3647 [2020-10-04]. ISSN 1435-9855. doi:10.4171/JEMS/909. (原始内容存档 (PDF)于2020-03-09) (英语).
- ^ Ringel, G. Theory of Graphs and its Applications. Proceedings of the Symposium Smolenice. 1963.
- ^ Montgomery, Richard; Pokrovskiy, Alexey; Sudakov, Benny. A proof of Ringel's Conjecture. 2020-01-08. arXiv:2001.02665 [math.CO].
- ^ Hartnett, Kevin. Rainbow Proof Shows Graphs Have Uniform Parts. Quanta Magazine. [2020-02-20]. (原始内容存档于2020-02-20) (英语).
- ^ Tichy, Robert F.; Wagner, Stephan, Extremal problems for topological indices in combinatorial chemistry (PDF), Journal of Computational Biology, 2005, 12 (7): 1004–1013 [2020-10-04], PMID 16201918, doi:10.1089/cmb.2005.12.1004, (原始内容存档 (PDF)于2017-09-21).
- ^ Oswin Aichholzer. Rectilinear Crossing Number project. [2020-10-04]. (原始内容存档于2007-04-30).
- ^ Robertson, Neil; Seymour, P. D.; Thomas, Robin, Linkless embeddings of graphs in 3-space, Bulletin of the American Mathematical Society, 1993, 28 (1): 84–89, MR 1164063, arXiv:math/9301216 , doi:10.1090/S0273-0979-1993-00335-5.
- ^ Conway, J. H.; Cameron Gordon. Knots and Links in Spatial Graphs. J. Graph Th. 1983, 7 (4): 445–453. doi:10.1002/jgt.3190070410.
