柱化異相雙三角柱
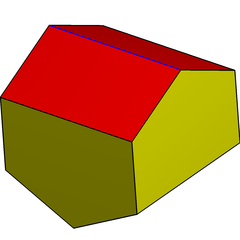
在幾何學中,柱化異相雙三角柱或山牆菱面體是一種空間填充多面體[1], 由4個矩形和4個直角五邊形組成,為八面體的一種,可以視為將異相雙三角柱的三角形之底邊向下拉長成五邊形所形成的立體。[2]
 | |||
| 對偶多面體 | 扭稜鍥形體 | ||
|---|---|---|---|
| 名稱 | 柱化異相雙三角柱 elongated gyrobifastigium | ||
| 性質 | |||
| 面 | 8 | ||
| 邊 | 18 | ||
| 頂點 | 12 | ||
| 歐拉特徵數 | F=8, E=18, V=12 (χ=2) | ||
| 組成與佈局 | |||
| 面的種類 | 4個矩形 4個五邊形 | ||
| 頂點佈局 | (4) 4.4.5 (8) 4.5.5 | ||
| 對稱性 | |||
| 對稱群 | D2d, [2+,4], (2*2), order 8 | ||
| 旋轉對稱群 | D2, [2,2]+, (222), order 4 | ||
| 圖像 | |||
| |||
名稱
编辑柱化異相雙三角柱的名稱來自正多邊形面的異相雙三角柱,因為柱化異相雙三角柱可以視為將異相雙三角柱的4個三角形面以「柱化」[註 1]的方式拉長成五邊形。 其英語名稱elongated gyrobifastigium的fastigium來自拉丁語fastigium,義為傾斜的屋頂,用以描述柱化異相雙三角柱的外觀[3]。 在標準的詹森多面體命名中,雙三角柱的雙(bi-)代表立體由2個三角柱組合而成,而異相(gyro-)則代表2個三角柱疊合時的方向不同,柱化(elongated)則在表在兩立體疊合的中間加入柱體使其被「拉長」。 若將三角柱以矩形側面為底,則在該底的對邊會一一條稜,將這條稜視為一個二角形上底可以令這個三角柱成為一種帳塔,該帳塔的底面為二角形,此時,柱化異相雙三角柱可以視為異相雙帳塔柱的一員,因此柱化異相雙三角柱也可以稱為異相雙二角帳塔柱。
幾何
编辑柱化異相雙三角柱共由8個面、18條邊和12個頂點所組成。其最高的對稱性形式是8階的D2d群,而若下方的長方體變為菱面體,則對稱性降為2重旋轉對稱、2階的C2群。
柱化異相雙三角柱所有的頂點之分支度皆為3,因此其對偶多面體所有面皆為三角形,也存在一種形式的柱化異相雙三角柱對應的對偶多面體為所有面皆為正三角形的扭稜鍥形體。[5]但該種柱化異相雙三角柱(扭稜鍥形體的對偶多面體)並非空間填充多面體,因為其五邊形不是直角五邊形。
相關形狀
编辑等面十三胞體是一種胞形狀為柱化異相雙三角柱的多胞體,其可以透過取13-5階棱柱(13-5 step prism)的對偶多胞形來構造,並具有扭稜鍥形體形的頂點圖。[6]
變體
编辑有一種拓樸獨特的柱化異相雙三角柱具有正方形和正三角形面,這種柱化異相雙三角柱可以看做是兩個三角柱疊在一個中心立方體上。這樣的組合可以看作是一個所有面都是正多邊形的立體,但因為有兩兩共面的情況,因此不屬於詹森多面體[7] ,但可以被歸類在條件邊正多邊形凸多面體(一種擬詹森多面體,參閱條件邊正多邊形凸多面體)[8]。
| 三角形與正方形共面 |
基於這種方式(中心長方體加上下三角柱「屋頂」)構成的柱化異相雙三角柱可以獨立填充空間,但前提是其必須基於長方體或菱面體;其「屋頂」的角度則沒有限制,甚至可以是凹的。如果屋頂的角度為0,則該立體與立方體或長方體無異。
此外,組成柱化異相雙三角柱的側面五邊形也可以是正五邊形,此時「屋頂」的矩形會變為梯形 ,但這樣的柱化異相雙三角柱並不具備空間填充多面體的特性。
| 種類 | 空間填充多面體 | 非空間填充 | ||||
|---|---|---|---|---|---|---|
| 圖象 | 等邊五邊形 |
菱形 |
共面 |
凹 |
扭稜鍥形體的對偶多面體 |
正五邊形 |
| 展開圖 | ||||||
參見
编辑註釋
编辑參考文獻
编辑- ^ Weisstein, Eric W. (编). Gabled Rhombohedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Weisstein, Eric W. (编). Elongated Gyrobifastigium. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Rich, Anthony, Fastigium, Smith, William (编), A Dictionary of Greek and Roman Antiquities, London: John Murray: 523–524, 1875.
- ^ Goldberg, Michael, On the space-filling octahedra, Geometriae Dedicata, January 1981, Volume 10, Issue 1, pp 323–335 [1] (页面存档备份,存于互联网档案馆) PDF 互联网档案馆的存檔,存档日期2017-12-22.
- ^ Dual of Snub Disphenoid (J84). www.software3d.com. [2023-08-24]. (原始内容存档于2023-06-18).
- ^ 13 Sides: Tridecachoron. [2023-08-24]. (原始内容存档于2023-03-26).
- ^ Convex regular-faced polyhedra with conditional edges: P3,2. [2023-08-24]. (原始内容存档于2019-03-23).
- ^ Robert R Tupelo-Schneck. Convex regular-faced polyhedra with conditional edges. [2023-01-31]. (原始内容存档于2021-08-18).

