样条函数
在数学学科数值分析中,样条(spline)是一种特殊的函数,由多项式分段定义。样条的英语单词spline来源于可变形的样条工具,那是一种在造船和工程制图时用来画出光滑形状的工具。在中国大陆,早期曾经被称做齿函数。后来因为工程学术语中放样一词而得名。
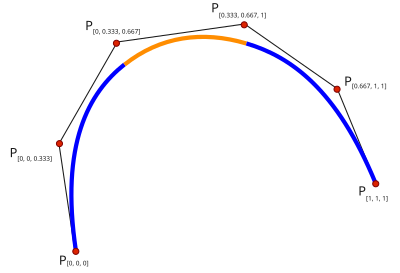
在插值问题中,样条插值通常比多项式插值好用。用低阶的样条插值能产生和高阶的多项式插值类似的效果,并且可以避免被称为龙格现象的数值不稳定的出现。并且低阶的样条插值还具有“保凸”的重要性质。
在计算机科学的计算机辅助设计和计算机图形学中,样条通常是指分段定义的多项式参数曲线。由于样条构造简单,使用方便,拟合准确,并能近似曲线拟合和交互式曲线设计中复杂的形状,样条是这些领域中曲线的常用表示方法。
定义
编辑设 为 上的区间,给定k个点ti,称为节点(knot),要求满足以下条件
设 为参数曲线。如果 ,并且S在每个子区间 上为n次多项式,则 称为n次样条。
称为节点值而 称为内部控制点(internal control point)。 称为节点向量(knot vector)。如果节点等距分布在区间 上,我们称样条均匀(uniform),否则为非均匀(non-uniform)。
注解
编辑对于一个给定的节点向量,所有n次样条构成一个向量空间。这个空间的一个基是n次B样条基。该空间的维数可从节点向量的数量得出:
维数等于次数与所有重复度的和:
如果样条有其他的线性限制条件,那么这个样条将存在于一个线性子空间中。例如自然三次样条的空间是C2三次样条的子空间。
常用的样条有许多种,由它们的特征命名。以下列出其中几种:
由表达方式命名:
- 如果样条是基曲线的线性组合, 则称为B样条
- 如果每个子区间的多项式由伯恩施坦多项式表达,则称为貝茲样条(Bézier splines)
由节点的特征命名:
- 若使用单个节点,每个子区间长度相等且Cn−1连续,则称为均匀样条(uniform splines)
- 若对子区间长度没有要求则称为非均匀样条(nonuniform splines)
由特殊条件限制命名:
- 若要求在a与b二次导数为零则称为自然样条(natural splines)
- 若要求样条曲线穿过实际数据点则称为插值样条(interpolating splines)
历史
编辑在计算机被使用之前,数字演算用手工完成。虽然分段定义的象signum函数或阶梯函数这样的函数也被用到,一般人更喜欢多项式因为它们比较容易算。随着计算机的发展,样条变得越来越重要。它们一开始是作为多项式在插值中的替代品,后来又作为在计算机图形学中构造光滑和可变形状的工具。
spline function是一类分段(片)光滑、并且在各段交接处也有一定光滑性的函数。简称样条。样条一词来源于工程绘图人员为了将一些指定点连接成一条光顺曲线所使用的工具,即富有弹性的细木条或薄钢条。由这样的样条形成的曲线在连接点处具有连续的坡度与曲率。分段低次多项式、在分段处具有一定光滑性的函数插值就是模拟以上原理發展起来的,它克服了高次多项式插值可能出现的振荡现象,具有较好的数值稳定性和收敛性,由这种插值过程产生的函数就是多项式样条函数。
样条函数的研究始于20世纪中叶,到了60年代它与计算机辅助设计相结合,在外形设计方面得到成功的应用。样条理论已成为函数逼近的有力工具。它的应用范围也在不断扩大,不仅在数据处理、数值微分、数值积分、微分方程和积分方程数值解等数学领域有广泛的应用,而且与最优控制、变分问题、统计学、计算几何与泛函分析等学科均有密切的联系。
参看
编辑- 样条插值
- 厄尔密样条(Hermite spline)
- 三次厄尔密样条
- 基数样条(cardinal spline)
- Catmull-Rom样条
- Kochanek-Bartels样条
- B样条
- 非均匀有理B样条(non-uniform rational B-spline,NURBS)
- de Boor算法,计算B样条的一个有效方法
- 贝塞尔样条
外部链接
编辑- An Interactive Introduction to Splines (页面存档备份,存于互联网档案馆)
- Learning by Simulations (页面存档备份,存于互联网档案馆) Interactive simulation of various cubic splines