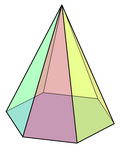
六角锥
在几何学中,六角锥是指底面为六边形的锥体,由六边形各个顶点向它所在的平面外一点依次连直线段而构成。所有六角锥皆为七面体,具有7个面、12个边和7个顶点,如同其他的锥体,对偶仍为六角锥,是一个自身对偶多面体。
 | ||
| 类别 | 锥体 | |
|---|---|---|
| 对偶多面体 | 六角锥(自身对偶) | |
| 数学表示法 | ||
| 康威表示法 | Y6 | |
| 性质 | ||
| 面 | 7 | |
| 边 | 12 | |
| 顶点 | 7 | |
| 欧拉特征数 | F=7, E=12, V=7 (χ=2) | |
| 组成与布局 | ||
| 面的种类 | 6个三角形(侧面) 1个六边形(底面) | |
| 顶点图 | 6(32.6) (36) | |
| 对称性 | ||
| 对称群 | C6v, [6], (*66) | |
| 旋转对称群 | C6, [6]+, (66) | |
| 特性 | ||
| 凸 | ||
| 图像 | ||
| ||
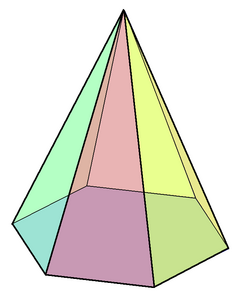
若一个六角锥的底面为正六边形则可称为正六角锥,但正六角锥不能算是詹森多面体,因为若每一个面都是正多边形的话,整个图形将会共平面,成为六阶三角形镶嵌的一部分。
正六角锥具有C6v对称性,并且使得其高与底面的交点与任意底面顶点和锥体顶部的顶点可构成直角三角形。
相关多面体与镶嵌
编辑| 正二棱锥 | 正三棱锥 | 正四棱锥 | 正五棱锥 | 正六棱锥 | 正七棱锥 | 正八棱锥 | 正九棱锥 | 正十棱锥 | ... | 圆锥 |
|---|---|---|---|---|---|---|---|---|---|---|
| 球面镶嵌 | 锥体 | 欧式镶嵌 仿紧空间 |
双曲镶嵌 非紧空间 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 一角锥 C1v, [1] |
二角锥 C2v, [2] |
三角锥 C3v, [3] |
四角锥 C4v, [4] |
五角锥 C5v, [5] |
六角锥 C6v, [6] |
七角锥 C7v, [7] |
八角锥 C8v, [8] |
九角锥 C9v, [9] |
十角锥 C10v, [10] |
... |
无限角锥 C∞v, [∞] |
超无限角锥 Ciπ/λv, [iπ/λ] |
参见
编辑外部链接
编辑- 埃里克·韦斯坦因. Hexagonal Pyramid. MathWorld.
- Virtual Reality Polyhedra(页面存档备份,存于互联网档案馆) www.georgehart.com: The Encyclopedia of Polyhedra
- Conway Notation for Polyhedra(页面存档备份,存于互联网档案馆) Try: "Y6"