维基百科

截角大星形十二面体

在几何学中，截角大星形十二面体又称小复杂截半二十面体（small complex icosidodecahedron）是一种退化的星形均匀多面体，由于其可以视为截角的大星形十二面体或过截角的大二十面体，其截角产生的棱两两互相重合，外观与正二十面体无异，但其有12个五边形面隐没在立体内部，通常需要借由让三角形面变透明才能看出整个立体的构造[2]。

截角大星形十二面体
截角大星形十二面体
类别退化均匀星形多面体
识别
鲍尔斯缩写
（verse-and-dimensions的wikia：Bowers acronym）		cid在维基数据编辑
数学表示法
考克斯特符号
（英语：Coxeter-Dynkin diagram）		node 3 node_1 5 rat d2 node_1 
施莱夫利符号t1,2{3,5/2}
威佐夫符号
（英语：Wythoff symbol）		5 | 3/2 5[1]
性质
面32
边60
顶点12
欧拉特征数F=32, E=60, V=12 （χ=-16）
组成与布局
面的种类12个五边形{5}
20个正三角形
面的布局
（英语：Face configuration）		12{5}+20{3}
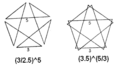
顶点图(3/2.5)5
(3.5)5/3
对称性
对称群Ih, [5,3], *532
图像

(3/2.5)5
(3.5)5/3
（顶点图）
将外层三角形面（红色）中间打洞的截角大星形十二面体，可以看到内侧互相相交的五边形面（黄色）。

性质 编辑

小复杂截半二十面体由12个五边形和20个正三角形组成，其共有32个面、60条边和12个顶点，若不计重合的边，则会导致立体中的每条棱都是四个面的公共棱[3]。这种立体是均匀多面体的一种退化形式，在考克斯特的书中，这种形式被以威佐夫记号5 | 3/2 5。[1]

作为复合多面体 编辑

小复杂截半二十面体可以视为正二十面体和大十二面体的复合多面体，由于正二十面体和大十二面体其顶点和边可以互相共用 [4]，其组成成的复合体也称为小复杂截半二十面体[5][6]

复合多面体
     
正二十面体 大十二面体 复合体

作为截角多面体 编辑

均匀截角即为一般用于产生半正多面体（如阿基米德立体）所用的截角变换[7][注 1]，其结果在考克斯特记号中可以用       表示[11] ，而套用了这种截角变换后会使得大星形十二面体转变成外观与一般正二十面体相同的立体，因此在绘制大星形十二面体十通长要是表面的正三角形透明化才能观察立体的整体。[2]

 

相关多面体 编辑

名称 大星形十二面体 截角大星形十二面体 大截半二十面体 截角大二十面体 大二十面体
考式（英语：Coxeter-Dynkin digram）                                        
图像          

与小复杂截半二十面体可以视为截角的大星形十二面体，与之类似的退化星形均匀多面体为另一个由星形正多面体截角的结果，其为截角小星形十二面体。[12]

星形正多面体 大十二面体 小星形十二面体 大二十面体 大星形十二面体
图像        
截角图像        
截角名称 截角大十二面体 截角小星形十二面体 截角大二十面体 截角大星形十二面体

小复杂截半二十面体由12个五边形和20个正三角形组成，另一种也是由12个五边形和20个正三角形组成立体为截半二十面体。[13]

参见 编辑

注释 编辑

  1. ^ 产生半正多面体所用的截角，即确保截角完后的面皆要等边的截角。[9][10]

参考文献 编辑

  1. ^ 1.0 1.1 Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P., Uniform polyhedra, Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences, 1954, 246: 401–450, ISSN 0080-4614, JSTOR 91532, MR 0062446, doi:10.1098/rsta.1954.0003  (Table 6, degenerate cases)
  2. ^ 2.0 2.1 Weisstein, Eric W. (编). Small Complex Icosidodecahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）. 
  3. ^ Uniforme Polyeder. math uni-bielefeld. [2019-09-22]. （原始内容存档于2019-09-22）. 
  4. ^ Paulo Freire's Polytopes. mpifr-bonn.mpg.de. [2019-09-22]. （原始内容存档于2020-12-04）. 
  5. ^ Norman Johnson. Guy Inchbald , 编. Polytopes - abstract and real (PDF). steelpillow. [2019-09-22]. （原始内容存档 (PDF)于2012-03-14）. 
  6. ^ Klitzing, Richard. cid, Polytopes & their Incidence Matrices. bendwavy.org. [2019-09-22]. （原始内容存档于2021-01-16）. 
  7. ^ Olshevsky, George, Truncation at Glossary for Hyperspace.
  8. ^ Coxeter, H.S.M.; Regular Polytopes (third edition). Dover Publications Inc. ISBN 0-486-61480-8
  9. ^ Coxeter, H.S.M. Chapter 8: Truncation, Regular Polytopes,[8] pp. 145–154
  10. ^ Norman Johnson, Uniform Polytopes, Manuscript (1991)
  11. ^ Coxeter, The Evolution of Coxeter-Dynkin diagrams, [Nieuw Archief voor Wiskunde 9 (1991) 233-248]
  12. ^ Maeder, Roman E. Uniform polyhedra. The Mathematica Journal (Citeseer). 1993, 3 (4): 48––57 [2019-09-22]. （原始内容存档于2021-08-23）. 
  13. ^ Weisstein, Eric W. (编). Icosidodecahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）. 
取自“https://zh.wikipedia.org/w/index.php?title=截角大星形十二面體&oldid=75152984”