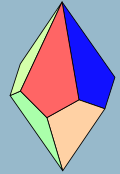
五方偏方面体
五方偏方面体是正十二面体的相对的两个面下面所接的棱延长交于一点所形成的多面体。[1][2]
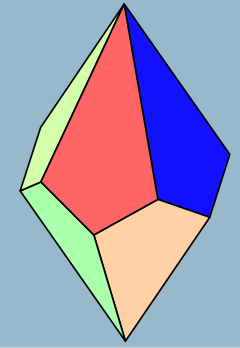 | |||
| 类别 | 偏方面体 | ||
|---|---|---|---|
| 对偶多面体 | 正五角反棱柱 | ||
| 数学表示法 | |||
| 考克斯特符号 | |||
| 性质 | |||
| 面 | 10 | ||
| 边 | 20 | ||
| 顶点 | 12 | ||
| 欧拉特征数 | F=10, E=20, V=12 (χ=2) | ||
| 组成与布局 | |||
| 面的种类 | 筝形 | ||
| 面的布局 | V5.3.3.3 | ||
| 对称性 | |||
| 对称群 | D5d, [2+,10], (2*5), order 20 | ||
| 旋转对称群 | D5, [2,5]+, (225), order 10 | ||
| 特性 | |||
| 凸、 面可递 | |||
| 图像 | |||
| |||
性质
编辑五方偏方面体共由10个面、20条边和12个顶点组成。组成五方偏方面体的10个面都是鸢形,而组成五方偏方面体的12个顶点有2个是5个鸢形的公共顶点,另外10个是3个鸢形的公共顶点。[3]
五方偏方面体有10个面,可用于游戏骰子,并于1906年获得专利。[4]由于这种骰子正好有10个面,因此经常应用于一些需要以百分位数计分的游戏。而正二十面体作为正多面体具有比五方偏方面体(非正多面体)更高的对称性,因此有时也会使用在正二十面体的20个面上标记2次0至9的数字代替五方偏方面体形状的骰子。
随后的十面骰子专利透过截去或圆滑化边缘对骰子的基本设计进行改善,其主要目的是增加骰子结果预测的难度。这个专利知名于1980年的Gen Con大会上[5],当时人们误认该专利涵盖了各种十面骰子。
相关多面体
编辑| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ... |
|---|---|---|---|---|---|---|---|---|---|---|---|
| |
|
|
|
|
|
|
|
|
|
|
|
| 球面投影 | |||||||||||
参考文献
编辑- ^ Cundy, H. M.; Rollett, A. P. Mathematical models 3rd. Oxford University Press. 1989: 117.
- ^ Richard Klitzing. pentagonal antidipyramid, pentagonal antitegum, pentagonal kiteohedron. bendwavy.org. [2022-12-30]. (原始内容存档于2022-12-30).
- ^ Dipyramids & Trapezohedra: Pentagonal Trapezohedron. dmccooey.com. [2022-12-29]. (原始内容存档于2022-12-29).
- ^ 美国专利第809,293号
- ^ Greg Peterson about Gen Con 1980: The big news of the year was that someone had 'invented' the ten-sided die.. (原始内容存档于2016-08-14).
| 这是一篇与多面体相关的小作品。您可以通过编辑或修订扩充其内容。 |