凸包
在一个实数向量空间中,对于给定集合,所有包含X的凸集的交集被称为的凸包。
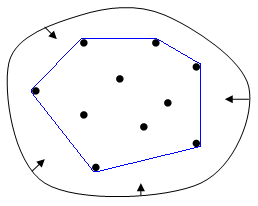
的凸包可以用内所有点的线性组合来构造。
在二维欧几里得空间中,凸包可想象为一条刚好包著所有点的橡皮圈。
演算法
编辑增量式算法
编辑逐次将点加入,然后检查之前的点是否在新的凸包上。由于每次都要检查所有之前的点,时间复杂度为 。
包裹法(Jarvis步进法)
编辑首先由一点必定在凸包的点开始,例如最左的一点 。然后选择 点使得所有点都在 的右方,这步骤的时间复杂度是 ,要比较所有点以 为原点的极坐标角度。以 为原点,重复这个步骤,依次找到 。这总共有 步。因此,时间复杂度为 。
葛立恒(Graham)扫描法
编辑由最底的一点 开始(如果有多个这样的点,那么选择最左边的),计算它跟其他各点的连线和x轴正向的角度,按小至大将这些点排序,称它们的对应点为 。这里的时间复杂度可达 。
考虑最小的角度对应的点 。若由 到 的路径相对 到 的路径是向右转的(可以想象一个人沿 走到 ,他站在 时,是向哪边改变方向),表示 不可能是凸包上的一点,考虑下一点由 到 的路径;否则就考虑 到 的路径是否向右转……直到回到 。
这个演算法的整体时间复杂度是 ,注意每点只会被考虑一次,而不像Jarvis步进法中会考虑多次。
这个演算法由葛立恒在1972年发明。[1]它的缺点是不能推广到二维以上的情况。
单调链
编辑将点按x坐标的值排列,再按y坐标的值排列。
选择x坐标为最小值的点,在这些点中找出y坐标的值最大和y坐标的值最小的点。对于x坐标为最大值也是这样处理。将两组点中y坐标值较小的点连起。在这条线段下的点,找出它们之中y坐标值最大的点,又在它们之间找x坐标值再最小和最大的点……如此类推。
时间复杂度是 。
将点集X分成两个不相交子集。求得两者的凸包后,计算这两个凸包的凸包,该凸包就是X的凸包。时间复杂度是 。
快包法(Akl-Toussaint启发式)
编辑选择最左、最右、最上、最下的点,它们必组成一个凸四边形(或三角形)。这个四边形内的点必定不在凸包上。然后将其馀的点按最接近的边分成四部分,再进行快包法(QuickHull)。
| 多面体名称 | 凸包 |
|---|---|
| 小星形十二面体 | 正二十面体 |
| 大十二面体 | 正二十面体 |
| 大星形十二面体 | 正十二面体 |
| 大二十面体 | 正十二面体 |
应用
编辑参考
编辑- ^ Graham, R.L. (1972). An Efficient Algorithm for Determining the Convex Hull of a Finite Planar Set. Information Processing Letters 1, 132-133
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0262032937. Pages 955–956 of section 33.3: Finding the convex hull.
- The Convex Hull of a 2D Point Set or Polygon, by Dan Sunday(页面存档备份,存于互联网档案馆)





