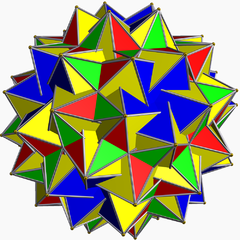
大扭稜十二面截半二十面體
大扭稜十二面截半二十面體(great snub dodecicosidodecahedron)是一種星形均勻多面體,由80個正三角形和24個正五角星組成[1],索引為U64,對偶多面體為大六角六十面体[2],具有二十面體群對稱性[3][1][4],並且與扭稜二十面化截半大十二面體拓樸同構[5],同時可以視為是大二重斜方截半二十面體的刻面多面體[5]。
 | ||||
| 類別 | 均勻星形多面體 | |||
|---|---|---|---|---|
| 對偶多面體 | 大六角六十面体 | |||
| 識別 | ||||
| 名稱 | 大扭稜十二面截半二十面體 great snub dodecicosidodecahedron great snub dodekicosidodecahedron | |||
| 參考索引 | U64, C80, W115 | |||
| 鮑爾斯縮寫 | gisdid | |||
| 數學表示法 | ||||
| 考克斯特符號 | ||||
| 威佐夫符號 | | 5/3 5/2 3 | |||
| 性質 | ||||
| 面 | 104 | |||
| 邊 | 180 | |||
| 頂點 | 60 | |||
| 歐拉特徵數 | F=104, E=180, V=60 (χ=-16) | |||
| 組成與佈局 | ||||
| 面的種類 | (20+60)個正三角形 (12+12)個正五角星 | |||
| 頂點圖 | 3.3.3.5/2.3.5/3 | |||
| 對稱性 | ||||
| 對稱群 | Ih, [5,3]+, 532 | |||
| 圖像 | ||||
| ||||
性質
编辑大扭稜十二面截半二十面體共由104個面、180條邊和60個頂點組成[3]。在其104個面中,有80個正三角形面和24個正五角星面[1],當中的80個正三角形面可以分成20個一般的正三角形面和60個在扭稜變換過程所產生的正三角形面[6];其24個正五角星面可以分成12個一般的正五角星面(施萊夫利符號:{5/2})和12個反向相接的正五角星面(施萊夫利符號:{5/3})[7]。在其60個頂點中,每個頂點都是2個正五角星面和4個正三角形面的公共頂點,並且這些面在構成頂角的多面角時,以反向相接的正五角星、正三角形、正五角星、正三角形、正三角形和正三角形的順序排列,在頂點圖中可以用(5/3.3.5/2.3.3.3)[8]或(3.5/3.3.5/2.3.3)[7][3]來表示。
表示法
编辑大扭稜十二面截半二十面體在考克斯特—迪肯符号中可以表示為 [9](s5/3s5/2s3*a)[10],在威佐夫記號中可以表示為| 5/3 5/2 3[11][3]。
尺寸
编辑若大扭稜十二面截半二十面體的邊長為單位長,則其外接球半徑為2平方根的倒數[5]或2平方根的一半:[2][1]
邊長為單位長的大扭稜十二面截半二十面體,中分球半徑為二分之一:[1]
由於球體無法相切於大扭稜十二面截半二十面體所有面上,因此大扭稜十二面截半二十面體不存在內切球,但可以分別計算正三角形面之面相切球的半徑與正五角星面之面相切球的半徑。[1]
邊長為單位長的大扭稜十二面截半二十面體正三角形面之面相切球的半徑為六的平方根的六分之一:[1]
- 正三角形面
邊長為單位長的大扭稜十二面截半二十面體正五角星面之面相切球的半徑為:[1]
- 正五角星面
二面角
编辑大扭稜十二面截半二十面體共有三種二面角,分別為兩種正五角星面和正三角形面的二面角以及一種正三角形面和正三角形面的二面角。[1]
其中一種正五角星面和正三角形面的二面角角度約為16.3度:[1]
而另一種正五角星面和正三角形面的二面角角度約為125.77度:[1]
另外一種二面角為正三角形面和正三角形面的二面角,其角度為負三分之一的反餘弦值,約為109.47度:[1]
相關多面體
编辑大扭稜十二面截半二十面體與大二重斜方截半二十面體共用相同的頂點、邊、20個正三角形面和其所有的五角星面[5],大扭稜十二面截半二十面體也與大二重扭稜二重斜方十二面體共用60個正三角形面。
其也與二十複合八面體共用相同的邊佈局。此外,大扭稜十二面截半二十面體也與二十複合四面半六面體的其中一個手性對應體共用20個正三角形面,另外60個正三角形面出現在另一個對映體中。
| 凸包 |
大扭稜十二面截半二十面體 |
大二重斜方截半二十面體 |
| 大二重扭稜二重斜方十二面體 |
二十複合八面體 |
二十複合四面半六面體 |
圖像
编辑| 傳統填充 |
相交偶數次為外部 |
參見
编辑參考文獻
编辑- ^ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 1.11 David I. McCooey. Self-Intersecting Snub Quasi-Regular Polyhedra: Great Snub Dodecicosidodecahedron. [2022-08-24]. (原始内容存档于2022-08-24).
- ^ 2.0 2.1 Weisstein, Eric W. (编). Great Snub Dodecicosidodecahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ 3.0 3.1 3.2 3.3 Maeder, Roman. 64: great snub dodecicosidodecahedron. MathConsult. [2022-08-24]. (原始内容存档于2022-08-24).
- ^ Paul Bourke. Uniform Polyhedra (80). Math Consult AG. October 2004 [2019-09-27]. (原始内容存档于2013-09-02).
- ^ 5.0 5.1 5.2 5.3 Richard Klitzing. icosidodecadodecahedron, ided. bendwavy.org. [2022-08-24]. (原始内容存档于2021-09-24).
- ^ Jonathan Bowers. Polyhedron Category 6: Snubs. polytope.net. (原始内容存档于2021-10-19).
- ^ 7.0 7.1 Zvi Har'El. Kaleido Data: Uniform Polyhedron #69, great snub dodecicosidodecahedron. harel.org.il. 2006-11-14 [2022-08-14]. (原始内容存档于2022-08-24).
- ^ Kovič, J. Classification of uniform polyhedraby their symmetry-type graphs (PDF). Int. J. Open Problems Compt. Math. 2012, 5 (4) [2022-08-24]. (原始内容存档 (PDF)于2022-08-14).
- ^ Klitzing, Richard. Axial-Symmetrical Edge-Facetings of Uniform Polyhedra (PDF). tic. 2002, 2 (4): 3 [2022-08-24]. (原始内容存档 (PDF)于2022-08-14).
- ^ Richard Klitzing. Icosahedral Symmetries uniform polyhedra, Polytopes & their Incidence Matrices. bendwavy.org. [2022-08-07]. (原始内容存档于2018-07-07).
- ^ V.Bulatov. great snub dodecicosidodecahedron. [2022-08-24]. (原始内容存档于2022-08-24).


