三面体
在几何学中,三面体(英文:Trihedron)是指由3个面组成的多面体。面为平面的三面体在三维空间不能存在,因为要至少四个顶点才能在三维空间形成具有体积的多面体,除非它的面是曲面,或是存在四维超球面。此外,有一种抽象射影多面体是三面体,即立方体半形[1]。
| 部分的三面体 | |
|---|---|
 三面形 |
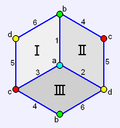 立方体半形 |
常见的三面体
编辑由于三维空间中的单纯形是四面体,因此面数少于4的多面体都只能成为退化多面体[2],因此三面体都不能真正具有体积。在球面镶嵌中,常见的三面体是三面形。亦有一种正抽象多面体是三面体,其为立方体半形。
三面形
编辑尽管面为平面的三面体在三维空间不能存在,但在球面几何学中,三面体可以以球面镶嵌的方式存在,最简单的例子是三面形。一个正三面形,表示三个镶嵌在球面上的球弓形,施莱夫利符号中利用{2,3}来表示,其对偶多面体是三角形二面体。[3]三面形是一种退化的三面体,无法拥有体积,由三个二角形组成。
三面形由三个二角形组成,每个顶点都是三个二角形的公共顶点。正三面形的每个面都是正二角形,且每个顶点都是三个正二角形的公共顶点,因此正三面形也可以视为一种正多面体,但是因为其已退化,因此不会与帕雷托立体一同讨论。
三面形具有D3h, [2,3], (*223)的对称性和D3, [2,3]+的旋转对称性,且阶数为12,在考克斯特符号中用 表示,其对称性与三角柱相同,因此三角柱也可以视为一种与三面形相关的立体,因为三角柱可以经由三面形透过截角变换构造。
二角锥
编辑二角锥是指底面为二角形的锥体,由于其底面为二角形,因此在欧几里得空间中,其已经退化无法拥有体积。在球面几何学中,其可以作为球面镶嵌,此时的二角锥由1个球面二角形和2个球面三角形构成,其可以视为在一条边上多加入一个顶点的三面形。这种二角锥共有3个面、4条边和3个顶点。二角锥的对偶多面体同样是二角锥,因此是一种自身对偶的多面体。
一角柱
编辑一角柱是指底面为一角形的柱体,由于其底面为一角形,因此在欧几里得空间中,其已经退化无法拥有体积。在球面几何学中,其可以作为球面镶嵌,此时的一角柱由两个球面一角形和一个球面四边形构成,等价于一面形经截角变换后的结果,因此又可称为截角一面形。这种一角柱共有3个面、3条边和2个顶点。一角柱的对偶多面体为双一角锥。
圆柱
编辑圆柱也能算是一种非严格的三面体,因为它可以看做是只有三个面的几何体,由一曲面(侧面)和两个圆形平面(底面)所组成。
三面体列表
编辑| 名称 | 种类 | 图像 | 符号 | 顶点 | 边 | 面 | χ | 面的种类 | 对称性 |
|---|---|---|---|---|---|---|---|---|---|
| 三面形 | 多面形 退化多面体 |
{2,3} |
2 | 3 | 3 | 2 | 3个二角形 | D3h, [2,3], (*223), order | |
| 二角锥 | 角锥 退化多面体 球面多面体 |
( )∨{2} | 3 | 4 | 3 | 2 | 1个二角形 2个三角形 |
C2v, [2] | |
| 一角柱 | 棱柱 退化多面体 |
t{2,1} {1}x{} |
2 | 3 | 3 | 2 | 2个一角形 1个矩形 |
D1h, [1,1], (*111), order 4 | |
| 皮特里正四面体 | 皮特里对偶 | {3,3}π | 4 | 6 | 3 | 1 | 3个正扭歪四边形 | ||
| 立方体半形 | 射影多面体 抽象多胞形 |
{4,3}/2 {4,3}3[4] |
4 | 6 | 3 | 1 | 3个正方形 | S4, order 24 | |
| {6,3}1,1 | 环形多面体 | {6,3}1,1 | 6 | 9 | 3 | 0 | 3个正六边形 | ||
| 圆柱体 | 非严格多面体 曲面 柱体 |
0 | 2 | 3 | 1 | 1个曲面 2个圆形 |
相关形状
编辑三胞体
编辑三胞体是指有三个胞或维面的多胞体。其为三面体在四维或更高维度的类比,但由于四维空间的单纯形是五胞体,任何面数边树或顶点数小于单纯形的图形都只能退化或成为球面镶嵌,即无法具有非零的体积。
参见
编辑参考文献
编辑- ^ McMullen, Peter; Schulte, Egon, 6C. Projective Regular Polytopes, Abstract Regular Polytopes 1st, Cambridge University Press: 162–165, December 2002, ISBN 0-521-81496-0
- ^ Sloane, N.J.A. (编). Sequence A135278 (Pascal's triangle with its left-hand edge removed). The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ The 3-hosohedron. weddslist.com. [2022-12-15]. (原始内容存档于2022-12-15).
- ^ N. Wedd. The hemicube. weddslist.com. 2010 [2016-08-14]. (原始内容存档于2019-05-02).