三面體
在幾何學中,三面體(英文:Trihedron)是指由3個面組成的多面體。面為平面的三面體在三維空間不能存在,因為要至少四個頂點才能在三維空間形成具有體積的多面體,除非它的面是曲面,或是存在四維超球面。此外,有一種抽象射影多面體是三面體,即立方體半形[1]。
| 部分的三面體 | |
|---|---|
 三面形 |
 立方體半形 |
常見的三面體
编辑由於三維空間中的單純形是四面體,因此面數少於4的多面體都只能成為退化多面體[2],因此三面體都不能真正具有體積。在球面鑲嵌中,常見的三面體是三面形。亦有一種正抽象多面體是三面體,其為立方體半形。
三面形
编辑儘管面為平面的三面體在三維空間不能存在,但在球面幾何學中,三面體可以以球面鑲嵌的方式存在,最簡單的例子是三面形。一個正三面形,表示三個鑲嵌在球面上的球弓形,施萊夫利符號中利用{2,3}來表示,其對偶多面體是三角形二面體。[3]三面形是一種退化的三面體,無法擁有體積,由三個二角形組成。
三面形由三個二角形組成,每個頂點都是三個二角形的公共頂點。正三面形的每個面都是正二角形,且每個頂點都是三個正二角形的公共頂點,因此正三面形也可以視為一種正多面體,但是因為其已退化,因此不會與柏拉圖立體一同討論。
三面形具有D3h, [2,3], (*223)的對稱性和D3, [2,3]+的旋轉對稱性,且階數為12,在考克斯特符號中用 表示,其對稱性與三角柱相同,因此三角柱也可以視為一種與三面形相關的立體,因為三角柱可以經由三面形透過截角變換構造。
二角錐
编辑二角錐是指底面為二角形的錐體,由於其底面為二角形,因此在歐幾里得空間中,其已經退化無法擁有體積。在球面幾何學中,其可以作為球面鑲嵌,此時的二角錐由1個球面二角形和2個球面三角形構成,其可以視為在一條邊上多加入一個頂點的三面形。這種二角錐共有3個面、4條邊和3個頂點。二角錐的對偶多面體同樣是二角錐,因此是一種自身對偶的多面體。
一角柱
编辑一角柱是指底面為一角形的柱體,由於其底面為一角形,因此在歐幾里得空間中,其已經退化無法擁有體積。在球面幾何學中,其可以作為球面鑲嵌,此時的一角柱由兩個球面一角形和一個球面四邊形構成,等價於一面形經截角變換後的結果,因此又可稱為截角一面形。這種一角柱共有3個面、3條邊和2個頂點。一角柱的對偶多面體為雙一角錐。
圓柱
编辑圓柱也能算是一種非嚴格的三面體,因為它可以看做是只有三個面的幾何體,由一曲面(側面)和兩個圓形平面(底面)所組成。
三面體列表
编辑| 名稱 | 種類 | 圖像 | 符號 | 頂點 | 邊 | 面 | χ | 面的種類 | 對稱性 |
|---|---|---|---|---|---|---|---|---|---|
| 三面形 | 多面形 退化多面體 |
{2,3} |
2 | 3 | 3 | 2 | 3個二角形 | D3h, [2,3], (*223), order | |
| 二角錐 | 角錐 退化多面體 球面多面體 |
( )∨{2} | 3 | 4 | 3 | 2 | 1個二角形 2個三角形 |
C2v, [2] | |
| 一角柱 | 棱柱 退化多面體 |
t{2,1} {1}x{} |
2 | 3 | 3 | 2 | 2個一角形 1個矩形 |
D1h, [1,1], (*111), order 4 | |
| 皮特里正四面體 | 皮特里對偶 | {3,3}π | 4 | 6 | 3 | 1 | 3個正扭歪四邊形 | ||
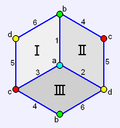
| 立方體半形 | 射影多面體 抽象多胞形 |
{4,3}/2 {4,3}3[4] |
4 | 6 | 3 | 1 | 3個正方形 | S4, order 24 | |
| {6,3}1,1 | 環形多面體 | {6,3}1,1 | 6 | 9 | 3 | 0 | 3個正六邊形 | ||
| 圓柱體 | 非嚴格多面體 曲面 柱體 |
0 | 2 | 3 | 1 | 1個曲面 2個圓形 |
相關形狀
编辑三胞體
编辑三胞體是指有三個胞或維面的多胞體。其為三面體在四維或更高維度的類比,但由於四維空間的單純形是五胞體,任何面數邊樹或頂點數小於單純形的圖形都只能退化或成為球面鑲嵌,即無法具有非零的體積。
參見
编辑參考文獻
编辑- ^ McMullen, Peter; Schulte, Egon, 6C. Projective Regular Polytopes, Abstract Regular Polytopes 1st, Cambridge University Press: 162–165, December 2002, ISBN 0-521-81496-0
- ^ Sloane, N.J.A. (编). Sequence A135278 (Pascal's triangle with its left-hand edge removed). The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ The 3-hosohedron. weddslist.com. [2022-12-15]. (原始内容存档于2022-12-15).
- ^ N. Wedd. The hemicube. weddslist.com. 2010 [2016-08-14]. (原始内容存档于2019-05-02).