形像理解凸函数与延森不等式
为某实向量空间的凸子集,若实值函数 对任意 及任意 ,皆有
-
则 称为凸函数。
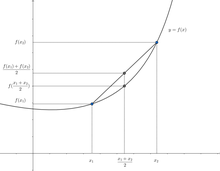
若 ,然后在 图像上任取两点 和 连线,则连线上某点 的 座标可以想成从 出发,前进了 这整段的一部分而已,也就是说
-
循著同样的比例 , 的 座标就可以写成
-
但同样的 座标下,对应的 函数值就是
-
所以,凸函数的定义意为, 的图像上,任意相异两点的连线不能低于中间 的曲线。[2]换言之,函数的上境图(图像上方的点的集合)为凸集。
若将定义的 号换成 ,则得到严格凸的定义:
称为严格凸,意思是对 和任意不相等的 ,皆有
-
若 ,在严格凸函数 的图像曲线上,任意两相异点的连线,除端点外皆高于曲线。
若 ,实值函数 对于任意三实数 ,都有 ,则称 是几乎凸的。
凸函数的某些性质,多元情况的叙述与一元情况同样简单。此种性质,可能仅于多元情况列举,恕不在一元情况赘述。
函数(蓝色)是凸的,当且仅当其上方的区域(绿色)是一个凸集。
- 设 是一元实函数,定义域为区间。考虑割线斜率 则函数 是对称函数,即关于 。 为凸,当且仅当对每个固定的 ,皆有 关于 单调不减(或由对称性,可将此句中 互换)。此刻划有助证明以下的结果。
- 若一元凸函数 定义在开区间 内,则在C内连续,且处处有左侧及右侧的单边导数。如此定义的两个单边导函数,皆为单调不减。由此推出,除可数个点外, 在其他点皆可微(不过不可导的点组成的集合,仍有可能稠密)。如果 是闭区间,那么 有可能在 的端点不连续,见例子。
- 一元可微函数在区间上是凸的,当且仅当函数位于所有它的切线的上方:[3]:69对于区间内的所有 和 ,都有 特别地,如果 ,则上式化为 ,故 是 的最小值。
- 一元可微函数在某个区间上是凸的,当且仅当它的导数在该区间上单调不减。若一元函数既凸又可导,则其导数也连续。
- 一元二阶可微的函数在区间上是凸的,当且仅当它的二阶导数是非负的;这是判断某个函数是否凸的实用方法。直观地,二阶可导的凸函数“向上弯”,而不会屈向另一边(即无拐点)。如果它的二阶导数是正数,那么函数就是严格凸的,但反过来不成立。例如, 的二阶导数是 ,当 时为零,但 是严格凸的。
- 此性质的条件“二阶导数非负”与前一个性质的条件“导数单调不减”有差异。若 在区间 非负,则的确 在 单调不减。反之则不然,因为可能有 在 单调不减,但在某点不可导,即 在 中某点无定义。
- 若 为一元凸函数,且 ,则 在正数集内为超可加函数,即 对任意正实数 成立。
更一般地,多元二次可微的连续函数在凸集上是凸的,当且仅当它的黑塞矩阵在凸集的内部是半正定的。
凸函数的任何极小值也是最小值。严格凸函数最多有一个最小值。
对于凸函数f,水平子集{x | f(x) < a}和{x | f(x) ≤ a}(a ∈ R)是凸集。然而,水平子集是凸集的函数不一定是凸函数;这样的函数称为拟凸函数。
延森不等式对于每一个凸函数f都成立。如果 是一个随机变量,在f的定义域内取值,那么 (在这里, 表示数学期望。)
- 如果 和 是凸函数,那么 和 也是凸函数。
- 如果 和 是凸函数,且 递增,那么 是凸函数。
- 凸性在仿射映射下不变:也就是说,如果 是凸函数( ),那么 也是凸函数,其中
- 如果 在 内是凸函数,且 是一个凸的非空集,那么 在 内是凸函数,只要对于某个 ,有 。
- 函数 处处有 ,因此f是一个(严格的)凸函数。
- 绝对值函数 是凸函数,虽然它在点x = 0没有导数。
- 当 时,函数 是凸函数。
- 定义域为[0,1]的函数f,定义为f(0)=f(1)=1,当0<x<1时f(x)=0,是凸函数;它在开区间(0,1)内连续,但在0和1不连续。
- 函数 的二阶导数为 ,因此它在x ≥ 0的集合上是凸函数,在x ≤ 0的集合上是凹函数。
- 每一个在 内取值的线性变换都是凸函数,但不是严格凸函数,因为如果f是线性函数,那么 。如果将“凸”替换为“凹”,该命题也成立。
- 每一个在 内取值的仿射变换,也就是说,每一个形如 的函数,既是凸函数又是凹函数。
- 每一个范数都是凸函数,这是由于三角不等式。
- 如果 是凸函数,那么当 时, 是凸函数。
- 和 为单调递增但非凸的函数。
- 函数f(x) = 1/x2,f(0)=+∞,在区间(0,+∞)内是凸函数,在区间(-∞,0)内也是凸函数,但是在区间(-∞,+∞)内不是凸函数,这是由于x = 0处的奇点。
- Moon, Todd. Tutorial: Convexity and Jensen's inequality. [2008-09-04]. (原始内容存档于2008-04-20).
- Rockafellar, R. T. Convex analysis. Princeton: Princeton University Press. 1970.
- Luenberger, David. Linear and Nonlinear Programming. Addison-Wesley. 1984.
- Luenberger, David. Optimization by Vector Space Methods. Wiley & Sons. 1969.
- Bertsekas, Dimitri. Convex Analysis and Optimization. Athena Scientific. 2003.
- Thomson, Brian. Symmetric Properties of Real Functions. CRC Press. 1994.
- Hiriart-Urruty, Jean-Baptiste, and Lemaréchal, Claude. (2004). Fundamentals of Convex analysis. Berlin: Springer.
- Krasnosel'skii M.A., Rutickii Ya.B. Convex Functions and Orlicz Spaces. Groningen: P.Noordhoff Ltd. 1961.
- Borwein, Jonathan, and Lewis, Adrian. (2000). Convex Analysis and Nonlinear Optimization. Springer.






![{\displaystyle \mathbb {E} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09de7acbba84104ff260708b6e9b8bae32c3fafa)
![{\displaystyle f(\mathbb {E} [X])\leq \mathbb {E} [f(X)],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fee18709fba0e49ef57d378c3299f5132d5c0b8c)