星 (圖論)
此條目的引用需要清理,使其符合格式。 (2019年5月23日) |
在圖論中,星(英語:Star)Sk屬於完全二分圖K1,k:是具有一個內部節點和k個葉節點的樹(但當k≤1時,沒有內部節點且由k+1個葉節點)。另外,一些文章將Sk 定義為最大直徑為2的k階樹;在這種情況下,k>2的星具有k−1個葉節點。
| 星 (圖論) | |
|---|---|
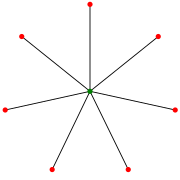 星S7 (一些文章認為這是星S8 )。 | |
| 頂點 | k+1 |
| 邊 | k |
| 直徑 | (2, k)的較小值 |
| 圍長 | ∞ |
| 色數 | (2, k+1)的較小值 |
| 色指數 | k |
| 屬性 | 邊傳遞 樹 單位距離 二分 |
有三條邊的星又稱為爪。
當k是偶數時,星Sk是邊優美圖,當k是奇數時則不是。它是一個邊傳遞的火柴杆圖,其直徑為2(當k > 1時),圍長為∞(無循環結構),色指數為k,色數為2(當k > 0時)。此外,星具有較大的自同構群,即k個字母上的對稱群。
與其他圖族的關係
編輯爪在無爪圖的定義中是很明顯的,這種圖的導出子圖沒有任何爪結構。[1][2]它們也是惠特尼圖同構定理的特例之一:一般來說,同構線圖除了爪與K3的特例外本身就是同構的。[3]
星是一種特殊的樹。與任何樹一樣,星可以由一個普呂弗序列編碼產生;普呂弗序列為Kk 的星由k − 1個中心點的複製形成。[4]
一些圖常量是用星來定義的。蔭度是一個圖表可以劃分成的最小森林數(森林裡的所有樹都是星)。圖的星色數是對頂點着色所需的最小顏色數,該着色使得任意兩個顏色類在一起均可形成一個所有連接組成部分都是星的子圖。[5][6]分支寬度為1的圖即是每個連接的組成部分都是星的圖。[7]
其他應用
編輯爪的頂點之間的距離集提供了一個有限度量空間的例子,這個有限度量空間不能被等距嵌入任何維度的歐氏空間。[8]
星型網是一種以星型圖為模型的計算機網絡,在分布式計算中占有重要地位。
利用星圖的一種幾何實現方法,即用一定長度的間隔來識別邊緣,是熱帶幾何中曲線圖常用的局部模型。熱帶曲線被定義為一個局部同構於星形度量圖的度量空間。
參考文獻
編輯- ^ Faudree, Ralph; Flandrin, Evelyne; Ryjáček, Zdeněk, Claw-free graphs — A survey, Discrete Mathematics, 1997, 164 (1–3): 87–147, MR 1432221, doi:10.1016/S0012-365X(96)00045-3
- ^ Chudnovsky, Maria; Seymour, Paul, The structure of claw-free graphs, Surveys in combinatorics 2005 (PDF), London Math. Soc. Lecture Note Ser. 327, Cambridge: Cambridge Univ. Press: 153–171, 2005 [2019-05-23], MR 2187738, (原始內容 (PDF)存檔於2012-10-23).
- ^ Whitney, Hassler, Congruent Graphs and the Connectivity of Graphs, American Journal of Mathematics, January 1932, 54 (1): 150–168, JSTOR 2371086, doi:10.2307/2371086.
- ^ Gottlieb, J.; Julstrom, B. A.; Rothlauf, F.; Raidl, G. R. https://web.archive.org/web/20060926171652/http://www.ads.tuwien.ac.at/publications/bib/pdf/gottlieb-01.pdf
|archive-url=缺少標題 (幫助) (PDF). GECCO-2001: Proceedings of the Genetic and Evolutionary Computation Conference. Morgan Kaufmann. 2001: 343–350 [2019-05-23]. ISBN 1558607749. 原始內容存檔於2006-09-26. - ^ Hakimi, S. L.; Mitchem, J.; Schmeichel, E. E., Star arboricity of graphs, Discrete Math., 1996, 149: 93–98, doi:10.1016/0012-365X(94)00313-8
- ^ Fertin, Guillaume; Raspaud, André; Reed, Bruce, Star coloring of graphs, Journal of Graph Theory, 2004, 47 (3): 163–182 [2019-05-23], doi:10.1002/jgt.20029, (原始內容存檔於2020-02-02).
- ^ Robertson, Neil; Seymour, Paul D., Graph minors. X. Obstructions to tree-decomposition, Journal of Combinatorial Theory, 1991, 52 (2): 153–190, doi:10.1016/0095-8956(91)90061-N.
- ^ Linial, Nathan, Finite metric spaces–combinatorics, geometry and algorithms, Proc. International Congress of Mathematicians, Beijing 3: 573–586, 2002, Bibcode:2003math......4466L, arXiv:math/0304466