星 (图论)
此条目的引用需要清理,使其符合格式。 (2019年5月23日) |
在图论中,星(英语:Star)Sk属于完全二分图K1,k:是具有一个内部节点和k个叶节点的树(但当k≤1时,没有内部节点且由k+1个叶节点)。另外,一些文章将Sk 定义为最大直径为2的k阶树;在这种情况下,k>2的星具有k−1个叶节点。
| 星 (图论) | |
|---|---|
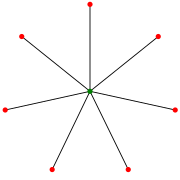 星S7 (一些文章认为这是星S8 )。 | |
| 顶点 | k+1 |
| 边 | k |
| 直径 | (2, k)的较小值 |
| 围长 | ∞ |
| 色数 | (2, k+1)的较小值 |
| 色指数 | k |
| 属性 | 边传递 树 单位距离 二分 |
有三条边的星又称为爪。
当k是偶数时,星Sk是边优美图,当k是奇数时则不是。它是一个边传递的火柴杆图,其直径为2(当k > 1时),围长为∞(无循环结构),色指数为k,色数为2(当k > 0时)。此外,星具有较大的自同构群,即k个字母上的对称群。
与其他图族的关系
编辑爪在无爪图的定义中是很明显的,这种图的导出子图没有任何爪结构。[1][2]它们也是惠特尼图同构定理的特例之一:一般来说,同构线图除了爪与K3的特例外本身就是同构的。[3]
星是一种特殊的树。与任何树一样,星可以由一个普吕弗序列编码产生;普吕弗序列为Kk 的星由k − 1个中心点的复制形成。[4]
一些图常量是用星来定义的。荫度是一个图表可以划分成的最小森林数(森林里的所有树都是星)。图的星色数是对顶点着色所需的最小颜色数,该着色使得任意两个颜色类在一起均可形成一个所有连接组成部分都是星的子图。[5][6]分支宽度为1的图即是每个连接的组成部分都是星的图。[7]
其他应用
编辑爪的顶点之间的距离集提供了一个有限度量空间的例子,这个有限度量空间不能被等距嵌入任何维度的欧氏空间。[8]
星型网是一种以星型图为模型的计算机网络,在分布式计算中占有重要地位。
利用星图的一种几何实现方法,即用一定长度的间隔来识别边缘,是热带几何中曲线图常用的局部模型。热带曲线被定义为一个局部同构于星形度量图的度量空间。
参考文献
编辑- ^ Faudree, Ralph; Flandrin, Evelyne; Ryjáček, Zdeněk, Claw-free graphs — A survey, Discrete Mathematics, 1997, 164 (1–3): 87–147, MR 1432221, doi:10.1016/S0012-365X(96)00045-3
- ^ Chudnovsky, Maria; Seymour, Paul, The structure of claw-free graphs, Surveys in combinatorics 2005 (PDF), London Math. Soc. Lecture Note Ser. 327, Cambridge: Cambridge Univ. Press: 153–171, 2005 [2019-05-23], MR 2187738, (原始内容 (PDF)存档于2012-10-23).
- ^ Whitney, Hassler, Congruent Graphs and the Connectivity of Graphs, American Journal of Mathematics, January 1932, 54 (1): 150–168, JSTOR 2371086, doi:10.2307/2371086.
- ^ Gottlieb, J.; Julstrom, B. A.; Rothlauf, F.; Raidl, G. R. https://web.archive.org/web/20060926171652/http://www.ads.tuwien.ac.at/publications/bib/pdf/gottlieb-01.pdf
|archive-url=缺少标题 (帮助) (PDF). GECCO-2001: Proceedings of the Genetic and Evolutionary Computation Conference. Morgan Kaufmann. 2001: 343–350 [2019-05-23]. ISBN 1558607749. 原始内容存档于2006-09-26. - ^ Hakimi, S. L.; Mitchem, J.; Schmeichel, E. E., Star arboricity of graphs, Discrete Math., 1996, 149: 93–98, doi:10.1016/0012-365X(94)00313-8
- ^ Fertin, Guillaume; Raspaud, André; Reed, Bruce, Star coloring of graphs, Journal of Graph Theory, 2004, 47 (3): 163–182 [2019-05-23], doi:10.1002/jgt.20029, (原始内容存档于2020-02-02).
- ^ Robertson, Neil; Seymour, Paul D., Graph minors. X. Obstructions to tree-decomposition, Journal of Combinatorial Theory, 1991, 52 (2): 153–190, doi:10.1016/0095-8956(91)90061-N.
- ^ Linial, Nathan, Finite metric spaces–combinatorics, geometry and algorithms, Proc. International Congress of Mathematicians, Beijing 3: 573–586, 2002, Bibcode:2003math......4466L, arXiv:math/0304466