規範形

數學和計算機科學中，數學對象的標準形、規範形是將該對象作為表達式呈現的標準方式。通常來說，它提供了對象的最簡單的表示，並允許以獨特的方式識別。「規範（canonical）」與「標準（normal）」的區別因領域而異，大多數時候規範形都規定了對象的唯一表示形式，而標準形則不要求唯一性。

以多重集為規範形進行算法易位構詞遊戲測試：以C語言數組形式給出字符串「madam curie」「radium came」。通過排序，將每個字符串竄轉為規範形。由於兩個字符串排序後完全相同，因此原字符串實為彼此的變形。

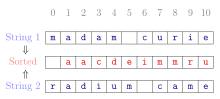
用小數表示，自然數的規範形是不以0開頭的有限數字序列。更一般地說，對於定義了等價關係的一類對象，規範形包括每類中的特定對象。例如

• 若爾當標準形是描述矩陣相似的規範形。
• 若將矩陣及其與可逆方陣的左乘視作等價，則階梯型矩陣是規範形。

在計算機科學與計算機代數中，在計算機中有很多方法表示同一個數學對象。這時，規範形是對每個對象都有唯一表示的表示法（典型化是將某種表示轉換為規範形的過程。因此，測試兩個對象的規範形是否相等，便可輕鬆地驗證它們是否等價。 規範形經常依賴於任意選擇（如變量排序），給測試兩個對象是否等價的獨立計算帶來困難。因此，在計算機代數中，標準形是很弱的概念：標準形中，0的表示是唯一的，因此可以通過對兩個對象作差、置於標準形中，來檢驗它們是否相等。

規範形也可以指以自然（規範）方式定義的微分形式。

定義

給定對象集合S以及其上的等價關係R ，則指定S中的一些對象為「規範形」，這樣所考慮的每個對象都等價於規範形的某個對象。換句話說S中的規範形代表一類等價類。要檢驗兩個對象是否等價，只需檢驗其規範形是否等價。 因此，規範形提供了分類定理，還為類中的對象提供了代表形式。

形式上，集合S上等價關係R的規範化是一個映射c:S→S，對所有s、s₁、s₂ ∈ S：

1. c(s) = c(c(s))   （冪等性）；
2. s₁ R s₂，若且唯若c(s₁) = c(s₂)   （決定性）；
3. s R c(s)  （代表性）。

性質3是冗餘的：將性質2應用於性質1即可得出。

在實際應用中，能識別規範形往往是有利的。還有一個實際的算法問題需要考慮：如何將S中的給定對象s轉換為規範形式s*？規範形一般用於更有效地運算等價類。例如，模算術中，同餘類的規範形通常是其中的最小非負整數。類運算可以組合這些代表形，並將結果還原為最小非負餘數。 唯一性要求有時會被放寬，允許形式在更精細的等價關係下是唯一的。

規範形可能只是慣例，也可能來自定理。例如，多項式在書寫時通常按冪次遞減：如x² + x + 30，而非x + 30 + x²。相對地，矩陣的若爾當標準形來自定理。

示例

大數記號

標準形用於書寫極大的數字，其中最知名的是科學計數法。

數論

• 正整數的規範表示
• 連分數的標準形

線性代數

對象	A等價於B的條件	規範形	註釋
複數正規矩陣	$A=U^{*}BU$，酉矩陣U	對角矩陣（重排序）	譜定理
複數矩陣	$A=UBV^{*}$，酉矩陣U、V	元素為正實數的對角陣（降序）	奇異值分解
代數閉域矩陣	$A=P^{-1}BP$，非奇異方陣P	若爾當標準形（塊重排序）
代數閉域矩陣	$A=P^{-1}BP$，非奇異方陣P	韋爾規範形（塊重排序）
域矩陣	$A=P^{-1}BP$，非奇異方陣P	弗羅貝尼烏斯標準形
主理想域矩陣	$A=P^{-1}BQ$，非奇異方陣P、Q	史密斯標準形	可逆的基本行列變換不影響等價性
整數矩陣	$A=UB$，么模矩陣U	埃爾米特標準形
整數模n矩陣		豪厄爾標準形
域K上的有限維向量空間	A、B作為向量空間同構	$K^{n}$，n為非負整數

代數

對象	A等價於B的條件	標準形
有限生成R-模，R為主理想域	A、B作為R-模同構	初等分解（重排序）或不變因子分解

幾何

解析幾何中：

• 直線方程：Ax + By = C，而 A² + B² = 1（C ≥ 0）
• 圓方程：$(x-h)^{2}+(y-k)^{2}=r^{2}$

方程還有其他書寫形式。例如，直線方程可以寫作點斜式和斜截式的一次方程。

凸多胞形可以表示為標準形：

• 所有面都是平的；
• 所有邊都與單位球面相切；
• 多面體的中心店位於原點。

可積系統

所有可微流形都有餘切叢，總可以被賦予某種微分形式，稱為重言1形式。這種形式使餘切叢具有辛流形的結構，並允許流形上的向量場通過歐拉-拉格朗日方程或哈密頓力學進行積分，這種可積的微分方程系統稱為可積系統。

動力系統

動力系統研究與可積系統有所重合；在動力系統研究中，我們也有標準形的概念。

三維幾何

三維流形研究中，有第一基本形式、第二基本形式與第三基本形式。

函數分析

對象	A、B等價的條件	標準形
希爾伯特空間	A、B均為有限維希爾伯特空間，則A、B保距同構。	$\ell ^{2}(I)$數列空間（將索引集I換為另一個等勢索引集的意義上）
有單位（unit）的可交換C*-代數	A、B作為C*-代數同構	緊豪斯多夫空間上的連續函數代數$C(X)$，與基空間同胚的意義上。

經典邏輯

主條目：規範形式 (布爾代數)

• 否定範式
• 合取範式
• 析取範式
• 代數範式
• 前束範式
• 斯科倫範式
• Blake範式，也稱為素蘊涵的完全和、完全和或析取素形式

集合論

• 序數的康托爾範式

改寫系統

改變公式的形式的符號操作稱為公式的「改寫」（rewriting）。可以研究可對公式進行有效操作的規則集合，以研究公式改寫的抽象性質，也就是「改寫規則」——抽象改寫系統的一個部分。常見問題是，有沒有可能將某些通用表達式變為一種單一的、通用的形式，即標準形。若不同的改寫序列仍能得到相同的形式，則這種形式就可稱為標準形，改寫則稱為匯合（confluent）。標準形不總可得。

λ演算

• 若不能進行beta還原，則lambda項就是Beta範式；λ演算是抽象改寫系統的一種特殊情況。例如，在無類型的lambda演算中，$(\lambda x.(xx)\;\lambda x.(xx))$項沒有標準形。在有類型的lambda演算中，每個形式良好的項都可改寫為標準形。

圖論

主條目：圖規範化

圖論中，圖規範化是找到給定圖G的規範形的過程。圖的規範形是與G圖同構的有標號圖Canon(G)，這樣，與G同構的圖都具有與G相同的規範圖，也就實現了圖同構的判斷。

計算 (計算機科學)

在計算中，將數據還原為任一種規範形通常稱為「數據規範化」（data normalization）。

例如，數據庫規範化是對關係數據庫的字段和數據庫表進行調整，以儘量減少數據冗餘與依賴的過程。 在軟件安全領域，常見的漏洞是未經檢查的惡意輸入（參見代碼注入），解決方法是進行適當的數據確認。在進行輸入驗證之前，通常會通過消除編碼（如HTML字符編碼）和將其化為單一通用字符編碼的方式進行正規化處理。 其他形式的數據（通常與信號處理，包括音頻、圖像，以及機器學習）也可以進行規範化處理，以將數值範圍框定得有限。

在內容管理中適用單一信源（SSOT）的概念，與數據庫規範化和軟件開發相仿。功能強大的內容管理系統可以提供獲取單一信源的合理方法，例如嵌入。

另見

• 典型化
• 規範基
• 標準叢
• 正則化
• 標準化

參考文獻

• Shilov, Georgi E., Silverman, Richard A. , 編, Linear Algebra, Dover, 1977, ISBN 0-486-63518-X .
• Hansen, Vagn Lundsgaard, Functional Analysis: Entering Hilbert Space, World Scientific Publishing, 2006, ISBN 981-256-563-9 .