超无限面形
超无限面形又称伪多面形(英语:pseudogonal hosohedron)或双曲无限面形(英语:Hyperbolic apeirogonal hosohedron)是一种双曲镶嵌,其相当于在双曲面上构造一个无限面形,因而导致在拓朴结构上该多面形之面数比无限面形还多[1],因此它在施莱夫利符号中用{2,iπ/λ}表示。
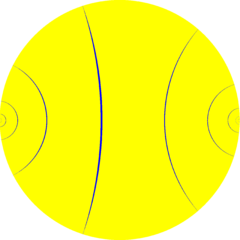 庞加莱圆盘模型 | ||
| 类别 | 双曲镶嵌 | |
|---|---|---|
| 对偶多面体 | 二阶超无限边形镶嵌 | |
| 数学表示法 | ||
| 考克斯特符号 | ||
| 施莱夫利符号 | {2,iπ/λ} | |
| 威佐夫符号 | 2 | iπ/λ 2 2 2 | iπ/λ | |
| 组成与布局 | ||
| 顶点图 | 2iπ/λ | |
| 对称性 | ||
| 对称群 | [iπ/λ,2], (*∞22) | |
| 旋转对称群 | [iπ/λ,2]+, (∞22) | |
| 特性 | ||
| 点可递、 边可递、 面可递、 发散 | ||
| 图像 | ||
| ||
超无限面形,是一种位于双曲平面上的正镶嵌图,可以视为多面形退化的类比,具有伪多边形群(pseudogonal group)的对称性,其考克斯特群为[iπ/λ,2],其可以视为无限面形在罗氏几何中的类比。
相关镶嵌
编辑超无限面形是多面形家族{2, p}的算术极限——无限面形在双曲空间的类比。
| 球面镶嵌 | 欧式镶嵌 仿紧空间 |
双曲镶嵌 非紧空间 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ... | ∞ | iπ/λ |
| 一面形 | 二面形 | 三面形 | 四面形 | 五面形 | 六面形 | 七面形 | 八面形 | 九面形 | 十面形 | 十一面形 | 十二面形 | 无限面形 | 超无限面形 | |
| {2,1} |
{2,2} |
{2,3} |
{2,4} |
{2,5} |
{2,6} |
{2,7} |
{2,8} |
{2,9} |
{2,10} |
{2,11} |
{2,12} |
{2,∞} |
{2,iπ/λ} | |
| 对称群:[iπ/λ,2], (*∞22) | [iπ/λ,2]+, (∞22) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| {iπ/λ,2} | t{iπ/λ,2} | r{iπ/λ,2} | 2t{iπ/λ,2}=t{2,iπ/λ} | 2r{iπ/λ,2}={2,iπ/λ} | rr{iπ/λ,2} | tr{iπ/λ,2} | sr{iπ/λ,2} | |||
| 半正对偶 | ||||||||||
| V∞2 | V2.∞.∞ | V2.∞.2.∞ | V4.4.∞ | V2∞ | V2.4.∞.4 | V4.4.∞ | V3.3.2.3.∞ | |||
参见
编辑参考文献
编辑- ^ Johnson, Norman W. 11.2 The polygonal groups. Geometries and transformations. Cambridge University Press. 2018: 141.
