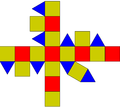
小斜方截半立方體

在幾何學中，小斜方截半立方體，又稱為菱方八面體，是一種有18個正方形和8個正三角形的阿基米德立體。小斜方截半立方體共有26個面、48條邊以及24個頂點，具有點可遞性質，因此既是均勻多面體也是半正多面體。

小斜方截半立方體

(按這裡觀看旋轉模型)
類別	半正多面體
對偶多面體	鳶形二十四面體
識別
名稱	小斜方截半立方體
參考索引	U10, C22, W13
鮑爾斯縮寫	sirco
數學表示法
考克斯特符號
施萊夫利符號	$r{\begin{Bmatrix}3\\4\end{Bmatrix}}$ rr{4,3}
威佐夫符號	3 4 | 2
康威表示法	eC aaC aaaT
性質
面	26
邊	48
頂點	24
歐拉特徵數	F=26, E=48, V=24 （χ=2）
組成與佈局
面的種類	正三角形 正方形
面的佈局	8個{3} (6+12)個{4}
頂點圖	3.4.4.4
對稱性
對稱群	Oh群
特性
-
圖像
3.4.4.4 （頂點圖） 鳶形二十四面體 （對偶多面體） （展開圖）

性質

小斜方截半立方體每八條棱可以成為一個正八邊形，共可以形成六個獨立的正八邊形。

體積與表面積

邊長為$a$的小斜方截半立方體，其表面積$A$和體積$V$如下：.

表面積$A=(18+2{\sqrt {3}})a^{2}\approx 21.4641016a^{2}$，

體積$V={\frac {1}{3}}(12+10{\sqrt {2}})a^{3}\approx 8.71404521a^{3}$。

座標

邊長為2且幾何中心位於原點的小斜方截半立方體，其頂點座標為：

$\left(\pm 1,\pm 1,\pm (1+{\sqrt {2}})\right)$

的全排列。邊長為1的小斜方截半立方體，其對偶多面體鳶形二十四面體的邊長為：

${\frac {2}{7}}{\sqrt {10-{\sqrt {2}}}}$ 和 ${\sqrt {4-2{\sqrt {2}}}}.\$

與其他幾何體的關聯

若將小斜方截半立方體扭曲使面不再是正多邊形，則它的頂點仍然會保持均勻。他們可以透過將立方體或八面體先截去所有的稜再截去所有的頂點而成，因此所得的多面體會有6個正方形面和12矩形面。他們具有八面體對稱並可以形成立方體和八面體之間的連續變形系列，類似於小斜方截半二十面體的變形或由四面體扭曲成的截半立方體。然而，小斜方截半立方體還具有另外的一系列不具有八面體對稱而是四面體對稱的變形，因此它們與四面體相同旋轉對稱但不同的反射對稱下是不變的，這些變體包含6個長方形面以及16個梯形面。若沿著三階魔術方塊的可轉動邊際投射到球體，則會的到一個與小斜方截半立方體類似的拓撲結構，小斜方截半立方體邊際的線條與該種圖形完全相同。事實上，有一些魔術方塊的變體就是小斜方截半立方體。

小斜方截半立方體能夠成三種空間均勻堆砌，但不能獨立完成堆砌，都要跟其他立體圖行一同完成堆砌。這三種空間均勻堆砌分別為：截棱立方體堆砌、截面斜截立方體堆砌以及截面立方體堆砌。

拆解

小斜方截半立方體可以被切割成上下兩個正四角帳塔和中間一個正八角柱。若將上下兩個正四角帳塔的其中一個水平旋轉45度的話，則會形成偽小斜方截半立方體，即異相雙四角台塔柱，它與小斜方截半立方體擁有相同的頂點布局：3.4.4.4。

小斜方截半立方體可以看作有三對互相平行的八邊形切面，因此上述的切割方式可以從三種不同的方式進行。其切割出來的正四角帳塔是一種詹森多面體。若將其切割出來的圖形，其中一個正四角帳塔水平旋轉45度之後重新組合則會形成一個看起來與小斜方截半立方體十分相近的不同立體，稱為異相雙四角台塔柱或偽小斜方截半立方體，其也是詹森多面體的一種。若將中間的正八角柱拿掉的話，小斜方截半立方體會變成同相雙四角台塔，而偽小斜方截半立方體會變成異相雙四角台塔，這兩個多面體也是詹森多面體。而這些屬於「異相」的多面體都是四角反稜柱的對稱性。

	小斜方截半立方體
	偽小斜方截半立方體

作法

將一個立方體（正八面體）十二條棱都切一刀，在八（六）個頂點處也切一刀，就可以得到一個小斜方截半立方體。該動作會先得到一個倒角立方體，然後再頂點處也切一刀後即得到小斜方截半立方體。

正交投影

小斜方截半立方體的正交投影

建立於	頂點	三角形-四邊形 交棱	四邊形-四邊形 交棱	正方形面		正三角形面
圖像
投影對稱性	[2]	[2]	[2]	[2]	[4]	[6]
對偶的正交投影

球面鑲嵌

	(6) 以正方形為中心	(6) 另一種以正方形為中心	(8) 以正三角形為中心
平行投影	施萊格爾投影

黃鐵礦形對稱群

均勻的形狀

不均勻的形狀

不均勻的形狀

到在極限情況下會 變成一個二十面體 扭稜八面體： , 從兩個位置之一。

二複合二十面體 從兩個交替位置。

頂點排佈

共有三種多面體與小斜方截半立方體有著相同的頂點排佈。他們分別為：

小斜方截半立方體

小立方立方八面體

小斜方六面體

星形截角立方體

應用

煤精印

由於小斜方截半立方體的形狀僅由正方形跟正三角形構成，且十分接近球體，繪製或製作都相對簡單，因此常出現在各種領域中，如藝術。

煤精印

煤精印外表是一個小斜方截半立方體，在正方形面18個，三角形面8個中，其中有14個正方形面上鐫刻有印文，小斜方截半立方體擁有26個面，也導致了該印章是目前已發現的中國古代多面印章中印面印章。小斜方截半立方體一共有18個正方形面，其中14個正方形面上印有「臣信上疏」、「臣信上章」、「臣信上表」、「臣信啟事」、「大司馬印」、「大都督印」、「刺史之印」、「柱國之印」、「耶勅」、「信啟事」、「信白箋」、「密」、「令」、「獨孤信白書」且皆為陰文楷書，它的發現證明早在南北朝時期，古人已經開始在印章中使用楷書，糾正了原先學界關於楷書入印最早為隋唐時期的觀點。

藝術

小斜方截半立方體出現在1495年盧卡·帕西奧利的肖像畫作中

達文西在帕西奧利神曲的設計 , 1509: "Vigintisexbasium Planum Vacuum".

較大的小斜方截半立方體出現在1495年盧卡·帕西奧利的肖像畫作中（傳統上對此畫作者有爭議，認為是雅各布·德巴爾巴里）。該畫作左上角有一個裝半滿水的小斜方截半立方體形狀的玻璃容器。首個有小斜方截半立方體的藝術畫作則是出現在達芬奇1509年的帕西奧利神曲。

雖然球形180×360°的全景可以投影到任何多面體，但小斜方截半立方體是一個更簡單更且十分近似球體的形狀，這種類型的投影，稱為斐洛球（英語：Philosphere），可用於全景圖合成成軟體中。部分能做成實體的全景圖合成成軟體是利用由單獨列印的兩個可利用剪刀剪下有留下黏貼處的圖像，即把全景圖製成小斜方截半立方體的展開圖，來做成斐洛球。

遊戲與玩具

一個Cabela's研發的能「自我修復」的防彈材料

遊戲《自由空間》中的關卡〈鑽井機〉和〈黑暗之地〉遊戲中的地圖形狀是一個小斜方截半立方體。

在超級馬里奧銀河的〈慌張銀河〉關卡中也有一個小斜方截半立方體形狀的行星。

魔棍解成球形的樣子，外觀類似小斜方截半立方體

《音速小子3》的Icecap Zone關卡也有以小斜方截半立方體為特色的柱子。

此外，由於三階魔術方塊的切割處（可旋轉的面）與小斜方截半立方體的邊際同構，或者說，將小斜方截半立方體的邊際投影至球體與三階魔術方塊的切割處投影至球體完全一致，因此外型為小斜方截半立方體形式的魔術方塊可以是一種三階魔術方塊的變體。

魔術方塊在1980年代流行期間，twisty puzzle曾經發售過小斜方截半立方體形式的魔術方塊。

魔術方塊的變體魔棍玩具在販售時通常會將其轉成小斜方截半立方體的形狀出售，12個方塊被替換成1：√2的矩形。

Cabela's研發的能「自我修復」的防彈材料如右圖，其示範的模形形狀與小斜方截半立方體十分接近。

相關多面體及鑲嵌

對稱性: [4,3], (*432)								[4,3]+ (432)	[1+,4,3] = [3,3] (*332)		[3+,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{31,1}	t{3,4} t{31,1}	{3,4} {31,1}	rr{4,3} s2{3,4}	tr{4,3}	c{4,3}	sr{4,3}	h{4,3} {3,3}	h2{4,3} t{3,3}	s{3,4} s{31,1}
		=	=	=					= or	= or	=
對偶多面體
V43	V3.82	V(3.4)2	V4.62	V34	V3.43	V4.6.8	V4.62/63	V34.4	V33	V3.62	V35

參見

• 立方體

參考文獻

1. Williams, Robert. The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. 1979. ISBN 0-486-23729-X.  (Section 3-9)
2. Cromwell, P. Polyhedra. United Kingdom: Cambridge. 1997: 79–86 Archimedean solids. ISBN 0-521-55432-2. 
3. Coxeter, H.S.M.; Longuet-Higgins, M.S.; Miller, J.C.P. Uniform Polyhedra. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences. May 13, 1954, 246 (916): 401–450. Bibcode:1954RSPTA.246..401C. doi:10.1098/rsta.1954.0003. 
4. de Graaf, J.; van Roij, R.; Dijkstra, M., Dense Regular Packings of Irregular Nonconvex Particles, Phys. Rev. Lett., 2011, 107: 155501, Bibcode:2011PhRvL.107o5501D, arXiv:1107.0603 , doi:10.1103/PhysRevLett.107.155501 
5. Betke, U.; Henk, M., Densest Lattice Packings of 3-Polytopes, Comput. Geom., 2000, 16: 157, doi:10.1016/S0925-7721(00)00007-9 
6. Torquato, S.; Jiao, Y., Dense packings of the Platonic and Archimedean solids, Nature, 2009, 460: 876, Bibcode:2009Natur.460..876T, PMID 19675649, arXiv:0908.4107 , doi:10.1038/nature08239 
7. Hales, Thomas C., A proof of the Kepler conjecture, Annals of Mathematics, 2005, 162: 1065, doi:10.4007/annals.2005.162.1065 

外部連結

• 埃里克·韋斯坦因, 小斜方截半立方體 （參閱阿基米德立體） 於MathWorld（英文）
  • 埃里克·韋斯坦因. Small rhombicuboctahedral graph. MathWorld. 
• Klitzing, Richard. 3D convex uniform polyhedra x3o4x - sirco. bendwavy.org. 
• The Uniform Polyhedra （頁面存檔備份，存於網際網路檔案館）
• Virtual Reality Polyhedra （頁面存檔備份，存於網際網路檔案館） The Encyclopedia of Polyhedra
• Editable printable net of a rhombicuboctahedron with interactive 3D view （頁面存檔備份，存於網際網路檔案館）
• Rhombicuboctahedron Star （頁面存檔備份，存於網際網路檔案館） by Sándor Kabai, Wolfram Demonstrations Project.
• Rhombicuboctahedron: paper strips for plaiting （頁面存檔備份，存於網際網路檔案館）