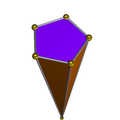
五角锥
五角锥是指底面为五边形的锥体。五角锥可以根据底面的特性分类,例如凹五角锥、凸五角锥和正五角锥。所有五角锥皆由6个面、10条边和6个顶点组成。[1]若一个正五角锥侧面也由正多边形组成,则这个立体是一种约翰逊多面体。在化学中,部分化学物质的分子形状为五角锥形,例如六甲苯的双电子离子。
 五角锥 | |||
| 类别 | 锥体 | ||
|---|---|---|---|
| 对偶多面体 | 五角锥(自身对偶) | ||
| 性质 | |||
| 面 | 6 | ||
| 边 | 10 | ||
| 顶点 | 6 | ||
| 欧拉特征数 | F=6, E=10, V=6 (χ=2) | ||
| 组成与布局 | |||
| 面的种类 | 5个三角形(侧面) 1个五边形(底面) | ||
| 特性 | |||
| 凸 | |||
| 图像 | |||
| |||
种类
编辑五角锥可以透过底面的性质进行分类。其中,底面为正五边形的五角锥称为正五角锥,特别地,若侧面也是正多边形,即正三角形,则属于约翰逊多面体;若底面为凹多边形称为凹五角锥;若底面为凸多边形称为凸五角锥。若高并非垂直于底面则称为斜五角锥,一般五角锥的侧面皆为等腰三角形,然而斜五角锥的侧面不完全是等腰三角形。[2]
-
五角锥(左)与斜五角锥(右)
正五角锥
编辑| 类别 | 约翰逊多面体 J1 - J2 - J3 | |
|---|---|---|
| 对偶多面体 | 正五角锥 (本身) | |
| 数学表示法 | ||
| 施莱夫利符号 | ()∨{5} | |
| 性质 | ||
| 面 | 6 | |
| 边 | 10 | |
| 顶点 | 6 | |
| 欧拉特征数 | F=6, E=10, V=6 (χ=2) | |
| 组成与布局 | ||
| 面的种类 | 5个正三角形 1个正五边形 | |
| 顶点布局 | 5(32.5) (35) | |
| 对称性 | ||
| 对称群 | C5v, [5], (*55) | |
| 旋转对称群 | C5, [5]+, (55) | |
| 特性 | ||
| 凸 | ||
| 图像 | ||
| ||
正五角锥是指底面为正五边形的五角锥体。[3]正五角锥由1个正五边形(底面)和5个三角形组成,共有10条边和6个顶点。在这6个顶点中有5个顶点是3个面(2个三角形和1个五边形)的公共顶点以及1个顶点是5个三角形的公共顶点。正五角锥具有五折锥体对称性。(C5v)[4]
-
侧面不为正三角形的正五角锥
-
所有面都是正多边形的正五角锥
对任意正五角锥而言,其侧面边长 与斜高 可透过底面边长 与高 来决定:[3]
此时这个高为 且底面边长为 的正五角锥表面积 与体积 为:[3]
约翰逊多面体
编辑若一个正五角锥底面和侧面皆为正多边形,则这种立体是一种约翰逊多面体(J2)中的一个。它能被看作为截角二十面体被截下的其中一块,或说是正二十面体被截成正五角锥反角柱(J11)所剩的锥体。1966年首先被诺曼·约翰逊命名、描述。[5]
若一正五角锥的底面和侧面都是正多边形,则其高可透过边长决定:
五角星锥
编辑五角星锥是指底面为五角星的五角锥,其是一种非凸多面体,因为这个立体的侧面与侧面互相相交。[7]这种星形五角锥可以在大十二面体上找到。[8]
使用
编辑在化学中,C
6(CH
3)2+
6的分子结构成五角锥形[12]。此外,当分子的原子落在五角锥上时,无论化学键的连接方式是否同于五角锥,都可以称之为五角锥型分子构型。例如XeOF−
5和IOF2−
5离子的分子构型皆为五角锥型。[13][14]
-
六甲苯的双电子离子(C
6(CH
3)2+
6)的分子棒状模型 -
五角锥型分子构型
五角锥型分子构型
编辑| 五角锥型分子构型 | |
|---|---|
| 举例 | XeOF− 5 |
| 点群 | C5v |
| 空间位数 | 7 |
| 配位数 | 6 |
| 键角 | 90°, 72° |
| 极性(μ) | >0 |
在化学中,五角锥型分子构型是指顶点原子正好依照五角锥的方式排列的分子结构。[15][16]在这个分子构型中,有6个原子、官能基或配基绕着中心原子排列,其中5个位于同一平面上,且中心原子带有一对孤电子对[17]:413–414。目前已知有两种离子的分子构型是五角锥形,分别是XeOF−
5离子[13]和IOF2−
5离子[13][14]。
这种分子构型是有着不均匀键角的少数分子键的其中一种。
五角锥型分子构型。粉红色代表中心原子、白色代表配基、黄色代表孤电子对
相关多面体与镶嵌
编辑五角锥是一种底面为五边形锥体[3],其他底面为多边形的锥体有:
| 正二棱锥 | 正三棱锥 | 正四棱锥 | 正五棱锥 | 正六棱锥 | 正七棱锥 | 正八棱锥 | 正九棱锥 | 正十棱锥 | ... | 圆锥 |
|---|---|---|---|---|---|---|---|---|---|---|
| 球面镶嵌 | 锥体 | 欧式镶嵌 仿紧空间 |
双曲镶嵌 非紧空间 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 一角锥 C1v, [1] |
二角锥 C2v, [2] |
三角锥 C3v, [3] |
四角锥 C4v, [4] |
五角锥 C5v, [5] |
六角锥 C6v, [6] |
七角锥 C7v, [7] |
八角锥 C8v, [8] |
九角锥 C9v, [9] |
十角锥 C10v, [10] |
... |
无限角锥 C∞v, [∞] |
超无限角锥 Ciπ/λv, [iπ/λ] |
五角锥也可以视为是正二十面体的一部分[18],类似地,星形五角锥可以视为是大十二面体的一部分。[8]另一方面,若将正二十面体的五角锥部分取下则会使得该立体成为五角锥反角柱[18]。五角锥反角柱可以视为是五角锥与五角反棱柱的组合,因此正二十面体也可视为为是一种双五角锥反角柱,也就是将五角反棱柱的两个五边形面替换成五角锥所形成的立体。[19]
参考文献
编辑- ^ 胡韵芝. 能從頂、棱和面的數目確定多面體的形狀嗎? (PDF). EduMath. 2005-06, 20 [2021-09-04]. (原始内容存档 (PDF)于2022-03-31).
- ^ 角錐與圓錐. 南一出版. [2021-09-04]. (原始内容存档于2022-03-14).
- ^ 3.00 3.01 3.02 3.03 3.04 3.05 3.06 3.07 3.08 3.09 Weisstein, Eric W. (编). Pentagonal Pyramid. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. [2020-04-12] (英语).
- ^ Johnson Solids: Regular Pentagonal Pyramid. dmccooey.com. [2021-09-04]. (原始内容存档于2021-09-04).
- ^ Johnson, Norman W., Convex polyhedra with regular faces, Canadian Journal of Mathematics, 1966, 18: 169–200, MR 0185507, Zbl 0132.14603, doi:10.4153/cjm-1966-021-8.
- ^ 6.0 6.1 Sapiña, R. Area and volume of a pentagonal pyramid and Johnson solid J₂. Problemas y ecuaciones. [2020-06-29]. ISSN 2659-9899. (原始内容存档于2021-11-13) (西班牙语).
- ^ Wenninger, Magnus J., Polyhedron Models, Cambridge University Press: 50, 1974, ISBN 978-0-521-09859-5, (原始内容存档于2013-12-11).
- ^ 8.0 8.1 立花彻美. 星形正多面体の正投象による基本図の作図. 図学研究 (日本図学会). 1987, 21 (3): 21–27.
- ^ “日研”新闻编集委员会 编‘茨城108景をめぐる’川崎松涛 监修、筑波书林、1991年9月20日:p.184
- ^ 茨城地方史研究会 编‘茨城の史迹は语る’瀬谷义彦・佐久间好雄 监修、茨城新闻社、1989年12月30日:pp.189 - 190
- ^ 中村哲夫‘茨城の建筑探访’仑书房出版、2006年5月20日. ISBN 4-8455-1127-4:pp.52 - 53
- ^ Ritter, Stephen K. Six bonds to carbon: Confirmed. Chem. Eng. News. 19 December 2016, 94 (49): 13 [2021-08-29]. doi:10.1021/cen-09449-scicon007. (原始内容存档于2017-01-09).
- ^ 13.0 13.1 13.2 Baran, E. Mean amplitudes of vibration of the pentagonal pyramidal XeOF−
5 and IOF2−
5 anions. J. Fluorine Chem. 2000, 101: 61–63. doi:10.1016/S0022-1139(99)00194-3. - ^ 14.0 14.1 Housecroft, Catherine E.; Sharpe, Alan G. Inorganic Chemistry 2nd. Pearson Prentice-Hall. 2005: 485. ISBN 0130-39913-2.
- ^ D. L. Kepert. Aspects of the Stereochemistry of Eight-Coordination. Progress in Inorganic Chemistry. 1978, 24: 179–249. doi:10.1002/9780470166253.ch4.
- ^ Von Zelewsky, A. Stereochemistry of Coordination Compounds. Chichester: John Wiley. 1995. ISBN 0-471-95599-X.
- ^ Petrucci, R. H.; W. S., Harwood; F. G., Herring. General Chemistry: Principles and Modern Applications 8th. Prentice-Hall. 2002. ISBN 978-0-13-014329-7.
- ^ 18.0 18.1 Weisstein, Eric W. (编). Gyroelongated pentagonal pyramid. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Kumar, CP. On the Coherent Labelling Conjecture of a Polyhedron in Three Dimensions. arXiv preprint arXiv:1801.08685. 2018.
- ^ Gunilla Borgefor. Uniform polyhedra, part 1. Centre for Image Analysis, Uppsala University, Sweden. [2021-09-06]. (原始内容存档于2021-09-06).
- ^ Hafner, Izidor. Dissection of small stellated dodecahedron and great stellated dodecahedron to rhombic triacontahedron and hexecontahedron. Visual Mathematics (Mathematical Institute SASA). 2007, (34).