十六面体
在几何学中,十六面体是指具有16个面的多面体。在十六面体当中没有任何一个形状是正多面体,换言之即正十六面体并不存在,但仍有存在一些等面或等角的十六面体,亦有一些十六面体皆由正多边形组成,例如正七角反棱柱、正五角锥反角柱、双四角锥反角柱等。常见的十六面体包括一些柱状和锥状的多面体,如十四角柱、十五角锥、正七角反棱柱、双八角锥和八方偏方面体等,亦有一些十六面体属于詹森多面体,即所有面皆由正多边形组成的多面体,例如正五角锥反角柱、双四角锥反角柱、侧锥十二面体等。部分半正多面体具有16个面,如正七角反棱柱和正十四角柱,但一般不会将这些多面体以“半正十六面体”称呼之。
| 部分的十六面体 | |
|---|---|
 七角帐塔 |
 侧锥十二面体 |
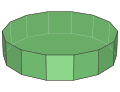 正十四角柱 |
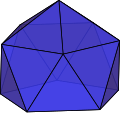 五角锥反角柱 |
凸十六面体
编辑所有十六面体中一共有387,591,510,244个拓扑不同构的凸十六面体,不包括镜像,并且至少需要包含10个顶点[1](如果两个多面体具有本质上不同的面排列、边与顶点的相接方式,则它们是“拓扑不同构”,因为如果两个立体间有不同的面排列、边与顶点的相接方式,则就无法仅透过改变边的长度或边或面之间的角度来将一个多面体形变成另一个)。
自身对偶十六面体
编辑所有十六面体中一共有302,404个自身对偶的十六面体,并且有1,476个自身对偶的十六面体有至少2阶的对称性[2]。高对称性的自身对偶十六面体具有手性四面体对称,其拓朴结构可以从移除正十二面体20顶点中的4个顶点所得的立体观察到,这立体又称欠四面二十面体。[3]
常见的十六面体
编辑十四角柱
编辑十四角柱是一种底面为十四边形的柱体,是十六面体的一种,其由16个面、28个顶点和42个边组成。正十四角柱代表每个面都是正多边形的十四角柱,其每个顶点都是2个正方形和1个十四边形的公共顶点,顶点图以 表示,在施莱夫利符号中可以利用{14}×{} 或 t{2, 14}来表示;在考克斯特—迪肯符号中可以利用 来表示;在威佐夫符号中可以利用2 14 | 2来表示;在康威多面体表示法中可以利用P14来表示。底边长为 、高为 的正十四角柱体积 和表面积 为[4]:
十五角锥
编辑十五角锥是一种底面为十五边形的锥体,是十六面体的一种,其具有16个面、30条边和16个顶点,其对偶多面体是自己本身[5]。正十五角锥是一种底面为正十五边形的十五角锥。底边长为 、高为 的正十五角锥体积 和表面积 为[5]:
七角反角柱
编辑七角反角柱是一种底面为七边形的反角柱,是十六面体的一种,其具有16个面、28条边和14个顶点[6],对偶多面体为七方偏方面体[7]。正七角反角柱是指所有面皆为正多边形的七角反角柱。若一个正七角反角柱边长为单位长,则其体积为:[7]
双四角锥反角柱
编辑双四角锥反角柱是一种以四边形为基底的角锥反角柱,是十六面体的一种,可以视为由两个四角锥以底面对底面地叠合到四角反棱柱的两个底面上所构成的立体,由16个三角形面、24条边和10个顶点所组成[8]。若双四角锥反角柱的基底为正方形,则这个立体称为正双四角锥反角柱。正双四角锥反角柱是一种詹森多面体,这意味着其所有的构成面都是正多边形,同时由于构成面皆为三角形,因此也是一种正三角面多面体。[9]
若双四角锥反角柱的边长为单位长,则其体积 和表面积 为:[10]
双八角锥
编辑双八角锥是一种以八边形为基底的双锥体,是十六面体的一种,其可以视为两个八角锥的底面对底面叠合成的立体,由16个面、24条边和10个顶点组成[11][12],对偶多面体为八角柱[12][13]。
双八角锥在施莱夫利符号中可以用{ }+{8}来表示,在考克斯特符号中可以用 来表示,在康威多面体表示法中可以用dP8来表示。
八方偏方面体
编辑八方偏方面体是一种以八边形为基底的偏方面体,是十六面体的一种,同时也是筝形多面体,是偏方面体系列的第六个成员,由十六个全等的筝形、32条边和18个顶点组成,对偶多面体是八角反角柱。[14][15]八方偏方面体的顶点有两种,分别为8个筝形的公共顶点和3个筝形的公共顶点。
八方偏方面体是一个等面图形,即面可递多面体,其所有面都相等。更具体来说,其不仅所有面都全等,且面与面必须能在其对称性上传递,也就是说,面必须位于同一个对称性轨道内。这种凸多面体是能做成公正的骰子的形状。[16]
八方偏方面体在施莱夫利符号中可以用{ }⨁{8}来表示,在考克斯特符号中可以用 或 来表示,在康威多面体表示法中可以用dA8来表示。
詹森多面体
编辑在詹森多面体中有3种立体具有十六个面[17],分别为五角锥反角柱、双四角锥反角柱和侧锥十二面体。
| 五角锥反角柱 |
双四角锥反角柱 |
侧锥十二面体 |
十六面体列表
编辑| 名称 | 种类 | 图像 | 符号 | 顶点 | 边 | 面 | χ | 面的种类 | 对称性 | 展开图 |
|---|---|---|---|---|---|---|---|---|---|---|
| 十四角柱 | 棱柱体 | t{2,14} {14}x{} |
28 | 42 | 16 | 2 | 2个十四边形 14个矩形 |
D14h, [14,2], (*14 2 2) | ||
| 十五角锥 | 棱锥体 | ( )∨{15} | 16 | 30 | 16 | 2 | 1个十五边形 15个三角形 |
C15v, [15], (*15 15) | ||
| 七角反棱柱 | 反棱柱 | s{2,14} sr{2,7} |
14 | 28 | 16 | 2 | 2个七边形 14个三角形 |
D7d, [2+,14], (2*7), 28阶 | ||
| 双八角锥 | 双锥体 | { }+{8} | 10 | 24 | 16 | 2 | 16个三角形 | D8h, [8,2], (*822), 32阶 | ||
| 七角帐塔 | 帐塔 | {7}||t{7} | 21 | 35 | 16 | 2 | 7个三角形 7个正方形 1个七边形 1个十四边形 |
C7v, [1,7], (*77), order 14 | ||
| 双四角锥反角柱 | 双锥反柱体 | 10 | 24 | 16 | 2 | 16个三角形 | D4d, [2+,4], (2*4) | |||
| 八方偏方面体 | 偏方面体 | { }⨁{8}[18] | 18 | 32 | 16 | 2 | 16个筝形 | D8d, [2+,8], (2*8) | ||
| 五角锥反角柱 | 角锥反角柱 | 11 | 25 | 16 | 2 | 15个三角形 1个五边形 |
C5v, [5], (*55) | |||
| 侧锥十二面体 | 侧锥正多面体 | 21 | 35 | 16 | 2 | 5个三角形 11个五边形 |
C5v | |||
| 欠四面十二面体 | 凸多面体 | 16 | 30 | 16 | 2 | 4个三角形 12个四边形 |
T, [3,3]+, (332), order 12 |
扭歪十六面体
编辑扭歪十六面体是指面与顶点并不存在同一个三维空间而无法确定体积的十六面体,扭歪十六面体仅能存在于四维或以上的空间。
而扭歪十六面体的一个例子为四角四片四角孔扭歪正十六面体,其由16个正方形组成,并且与四维超正方体共用相同的顶点布局。[19]
参见
编辑参考文献
编辑- ^ Counting polyhedra. numericana.com. [2022-08-28]. (原始内容存档于2016-05-06).
- ^ David I. McCooey. Symmetries of Canonical Self-Dual Polyhedra. [2022-08-28]. (原始内容存档于2013-10-05).
- ^ George W. Hart. Tetrahedrally Stellated Icosahedron. [2022-08-28]. (原始内容存档于2022-11-27).
- ^ Wolfram, Stephen. "Tetradecagonal prism". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- ^ 5.0 5.1 Wolfram, Stephen. "Pentadecagon pyramid". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- ^ Wolfram, Stephen. "heptagonal antiprism". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- ^ 7.0 7.1 David I. McCooey. Prisms & Antiprisms: Heptagonal Antiprism. [2022-08-28]. (原始内容存档于2016-03-04).
- ^ 8.0 8.1 David I. McCooey. Johnson Solids: Gyroelongated Square Dipyramid. [2022-08-28]. (原始内容存档于2022-08-28).
- ^ Nat Alison. Gyroelongated square bipyramid | J17. polyhedra.tessera.li. [2022-08-28]. (原始内容存档于2022-08-28).
- ^ 10.0 10.1 Weisstein, Eric W. (编). Gyroelongated Square Dipyramid. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ David I. McCooey. Dipyramids & Trapezohedra: Octagonal Dipyramid. [2022-08-28]. (原始内容存档于2022-08-28).
- ^ 12.0 12.1 David I. McCooey. Simplest Canonical Polyhedron with D8h Symmetry: Octagonal Dipyramid. [2022-09-14]. (原始内容存档于2022-09-14).
- ^ Wolfram, Stephen. "8‐dipyramid". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- ^ Wolfram, Stephen. "8-trapezohedron". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- ^ David I. McCooey. Dipyramids & Trapezohedra: Octagonal Trapezohedron. [2022-08-28]. (原始内容存档于2022-08-28).
- ^ McLean, K. Robin, Dungeons, dragons, and dice, The Mathematical Gazette, 1990, 74 (469): 243–256, JSTOR 3619822, doi:10.2307/3619822.
- ^ Johnson, Norman W. Convex Solids with Regular Faces. Canadian Journal of Mathematics. 1966, 18: 169–200. ISSN 0008-414X. Zbl 0132.14603. doi:10.4153/cjm-1966-021-8.
- ^ Johnson, N.W. Chapter 11: Finite symmetry groups. Geometries and Transformations. 2018. 11.3 Pyramids, Prisms, and Antiprisms, Figure 11.3c. ISBN 978-1-107-10340-5.
- ^ Klitzing, Richard. Skew polytopes x4o4o|xRo. bendwavy.org.