四角柱

在几何学中，四角柱又称四棱柱是指底面为四边形的柱体，当底面为正方形时会成为立方体。所有四角柱都有6个面8个顶点和12个边。对偶多面体是双四角锥。

四角柱

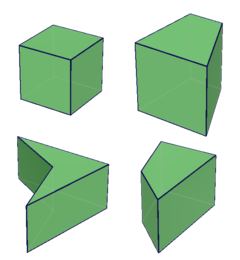四种四角柱
类别	柱体
对偶多面体	双四角锥
数学表示法
考克斯特符号
施莱夫利符号	t{2,4} {4}×{}
威佐夫符号	2 4 | 2
康威表示法	P4
性质
面	6
边	12
顶点	8
欧拉特征数	F=6, E=12, V=8 （χ=2）
组成与布局
面的种类	4个矩形侧面 2个四边形底面
顶点图	4.4.4
特性
凸

只要底面是四边形皆称为四角柱

性质

体积与表面积

底面为任意四边形的四角柱的体积可以利用底面积乘以高来计算，若底面为凸四边形则可以透过底面的两个对角线向量与两个底面对角线交点向量的三阶行列式绝对值来计算：

V_凸四角柱 = ${\frac {1}{2}}\left|{\begin{vmatrix}x_{{}_{AC}}&y_{{}_{AC}}&z_{{}_{AC}}\\x_{{}_{BD}}&y_{{}_{BD}}&z_{{}_{BD}}\\x_{{}_{PQ}}&y_{{}_{PQ}}&z_{{}_{PQ}}\end{vmatrix}}\right|$

其中ABCD为底面四边形，AC、BD为凸四角柱底面四边形的两条对角线，对角线AC向量为$(x_{{}_{AC}},y_{{}_{AC}},z_{{}_{AC}})$、对角线BD向量为$(x_{{}_{BD}},y_{{}_{BD}},z_{{}_{BD}})$，P为下底对角线交点、Q上底对角线交点，PQ为柱高，$(x_{{}_{PQ}},y_{{}_{PQ}},z_{{}_{PQ}})$表示PQ向量

亦可写为向量积与数量积的形式：

V_凸四角柱 = ${\frac {1}{2}}\left|{\overrightarrow {PQ}}\cdot ({\overrightarrow {AC}}\times {\overrightarrow {BD}})\right|$

此种计算方法源自于底面积乘以高，而任意凸四角柱的底面一定是凸四边形，因此会适用于任意凸四边形的面积公式，可由对角线长与对角线夹角计算

A_底面积$={\tfrac {1}{2}}{\overline {AC}}\,{\overline {BD}}\sin(\angle APB),$

而此公式就直接对应到底面对角线向量的外积：

${\overrightarrow {AC}}\times {\overrightarrow {BD}}=\left\|{\overrightarrow {AC}}\right\|\left\|{\overrightarrow {BD}}\right\|\sin(\angle APB)\ \mathbf {n}$

其中n为单位向量，但由于最后结果取绝对值所以被省略。

因此其表面积也可以利用此法计算，为底面积的两倍加上周长乘高：

A_凸四角柱 = $\left|{\overrightarrow {AC}}\times {\overrightarrow {BD}}\right|+(\left|{\overline {AB}}\right|+\left|{\overline {BC}}\right|+\left|{\overline {CD}}\right|+\left|{\overline {DA}}\right|)\cdot \mathbf {h}$

作为截角四面形

四面形是一种退化的四面体，在球面几何学中，四面形可以在球面上以镶嵌的方式存在，表示四个镶嵌在球体上的球弓形，施莱夫利符号中利用{2,4}来表示，然而四角柱可借由切去四面形的两个顶点产生上下两个四边形面，原本的二角形因为多了切去四面形的两个顶点所形成的两条边而变成侧面正方形。

也因此，四角柱在施莱夫利符号中也可以写为t{2,4}，表示截角的四面形。

四面形

截角四面形

常见的四角柱

正四角柱

正四角柱代表底面为正方形的四角柱，其对偶为正双四角锥。若侧面不是正方形也称为长方体，因为可以使用其中一个侧面当作底面。侧面也是正方形的正四角柱是正立方体，其具有正八面体对称性，对应的考克斯特群是BC₃对称性，由于底面和侧面全等，因此每个顶点都是三个正方形（一个底面正方形和两个侧面正方形）的公共顶点，施莱夫利符号{4,3}，其顶点图为正三角形，顶点布局为3³（三个正方形，一个底面和两个侧面），在考克斯特-迪肯符号中以表示，由于侧面是正方形的正四角柱是正多面体，因此其对偶多面体也会是正多面体，即正八面体，也就是一个所有面都全等的正双四角锥。

正四角柱

依照底面和侧面的特性有不同的对称性，对称性最高的是底面和侧面都是正方形的正四角柱，其次是侧面不是正方形的正四角柱，长宽高都不等长的长方体的对称性最低。

名称	立方体	正四角柱	长方体
考克斯特记号
施莱夫利符号	{4,3}	{4}×{}	{}×{}×{}
威佐夫记号	3 | 4 2	4 2 | 2	2 2 2 |
对称性	Oh (*432)	D4h (*422)	D2h (*222)
对称群阶数	24	16	8
图像	(111)	(112)	(123)

长方体

主条目：长方体

长方形的柱体称为长方体。其具有D_2h, [2,2], (*222)的对称性，阶数为8，其在施莱夫利符号中用{ } × { } × { }表示，其顶点图为三角形，在考克斯特-迪肯符号中以表示，其对偶多面体为双长方锥，及两个底面为长方体的四角锥被堆被堆叠所形成的立体。

若一个长方体的底面任一边长与与高相等，则这个长方体会有两个正方形侧面，因此也可以视为正四角柱，此时每个顶点都是2个长方形和一个正方形的公共顶点，具有点可递的性质，顶点图为等腰三角形，等腰三角形两个腰长来自长方形对角线，等腰三角形的底边来自正方形面，这种长方体在施莱夫利符号中可表示为{4}x{}、并具有比上述另一种长方体拥有更高的D_4h, [4,2], (*422)对称性，阶数为12。

其展开图的数量依边长的差异性有所不同。底面边长不同且高也跟底面边长不同的长方体共有54种不同的展开图。

四角柱

矩形柱的展开图

梯形柱

底面是梯形的四角柱称为梯形柱。

梯形柱

梯形柱

梯形柱展开图

梯形柱的体积可以借由LH(A + B)/2来计算，其中A是底面梯形的上底、B是底面梯形的下底、L是底面梯形的高、H是柱体的高。

非凸四角柱

非凸四角柱是指底面为非凸四边形的四角柱。

凹四角柱是指有一个角大于180度的四角柱，通常凹四角柱都是因为底面有凹四边形才会构成。

二复合二角形柱体 两个四边形二面体组成的复合体 在施莱夫利符号中计为{4/2}x{} 但是其已退化，不具有体积

凹筝形柱 底面为凹筝形的柱体

斜四角柱

斜四角柱是一种底面为四边形但是侧面与底面不成直角的柱体。最常见的斜四角柱是平行六面体，一种底面为平行四边形的斜四角柱。

斜平行四边形柱体 又称平行六面体

相关多面体与镶嵌

四角柱可以看作是一种截角四面形，其他与四面形相关的图形有：

半正方形二面体球面多面体

对称群：[4,2], (*422)							[4,2]+, (422)	[1+,4,2], (222)	[4,2+], (2*2)
{4,2}	t{4,2}	r{4,2}	2t{4,2}=t{2,4}	2r{4,2}={2,4}	rr{4,2}	tr{4,2}	sr{4,2}	h{4,2}	s{2,4}
半正对偶
V42	V82	V42	V4.4.4	V24	V4.4.4	V4.4.8	V3.3.3.4	V22	V3.3.2.3

四角柱是一个底面边数为四的柱体，底面边数不同的柱体有：

正多边形柱体系列

对称群	3	4	5	6	7	8	9	10	11	12
[2n,2] [n,2] [2n,2+]
图像
球面多面体
图像

柱体形式半正镶嵌系列：

球面镶嵌		柱体							欧式镶嵌 仿紧空间	双曲镶嵌 非紧空间
t{2,1}	t{2,2}	t{3,2}	{4,2}	t{5,2}	t{6,2}	t{7,2}	t{8,2}	...	t{2,∞}	t{2,iπ/λ}

立方体堆叠

立方体堆叠为立方体上下堆叠无限延伸的立体图形，可以看做是无限延伸的正四角柱，也就是其柱高为无穷的四角柱。沿着这种几何结构可以构造出一种扭歪无限边形，环绕着无限堆叠的正方体而构成一个四角螺旋无限边形，其扭曲角为90度，两条边之间的夹角为120度，在施莱夫利符号中以{∞}#{4}表示。

其也可以看作是立方体堆砌的一部分。

参见

• 六面体