拟詹森多面体
在几何学中,拟詹森多面体是严格凸多面体,其面几乎都是正多边形,但其中有部分或全部的面不是正多边形但很接近正多边形。 而拟詹森多面体经常会在正多边形与非正多边形之间有物理构造上可以忽略的微小差异[1]。近似的精确值取决于这样一个多面体的面逼近正多边形的程度。
| 部分的拟詹森多面体 | |
|---|---|
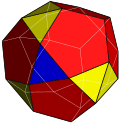 四阶十二面体 |
 部分截半截角八面体 |
 五边形六边形 五角十二面七十四面体 |
 截角三角化四面体 |
例子
编辑| 名称 康威多面体表示法 |
图像 | 顶点布局 | 顶点 | 边 | 面 | F3 | F4 | F5 | F6 | F8 | F10 | F12 | 对称性 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 底面截角双三角锥 t4dP3 |
2 (5.5.5) 12 (4.5.5) |
14 | 21 | 9 | 3 | 6 | Dih3 12阶 | ||||||
| 截角三角化四面体 t6kT |
4 (5.5.5) 24 (5.5.6) |
28 | 42 | 16 | 12 | 4 | Td, [3,3] 24阶 | ||||||
| 五边形六边形五角十二面七十四面体 | 12 (3.5.3.6) 24 (3.3.5.6) 24 (3.3.3.3.5) |
60 | 132 | 74 | 56 | 12 | 6 | Th, [3+,4] 24阶 | |||||
| 倒角立方体 cC |
24 (4.6.6) 8 (6.6.6) |
32 | 48 | 18 | 6 | 12 | Oh, [4,3] 48阶 | ||||||
| -- | 12 (5.5.6) 6 (3.5.3.5) 12 (3.3.5.5) |
30 | 54 | 26 | 12 | 12 | 2 | D6h, [6,2] 24阶 | |||||
| -- | 6 (5.5.5) 9 (3.5.3.5) 12 (3.3.5.5) |
27 | 51 | 26 | 14 | 12 | D3h, [3,2] 12阶 | ||||||
| 四阶十二面体 | 4 (5.5.5) 12 (3.5.3.5) 12 (3.3.5.5) |
28 | 54 | 28 | 16 | 12 | Td, [3,3] 24阶 | ||||||
| 部分截半截角八面体 | 24 (3.4.3.9) 24 (3.9.9) |
38 | 84 | 48 | 24 | 6 | Oh, [4,3] | ||||||
| 倒角十二面体 cD |
60 (5.6.6) 20 (6.6.6) |
80 | 120 | 42 | 12 | 30 | Ih, [5,3] 120阶 | ||||||
| 截半截角二十面体 atI |
60 (3.5.3.6) 30 (3.6.3.6) |
90 | 180 | 92 | 60 | 12 | 20 | Ih, [5,3] 120阶 | |||||
| 截角截角二十面体 ttI |
120 (3.10.12) 60 (3.12.12) |
180 | 270 | 92 | 60 | 12 | 20 | Ih, [5,3] 120阶 | |||||
| 扩展截角二十面体 etI |
60 (3.4.5.4) 120 (3.4.6.4) |
180 | 360 | 182 | 60 | 90 | 12 | 20 | Ih, [5,3] 120阶 | ||||
| 扭棱截角二十面体 stI |
60 (3.3.3.3.5) 120 (3.3.3.3.6) |
180 | 450 | 272 | 240 | 12 | 20 | I, [5,3]+ 60阶 |
共面拟詹森多面体
编辑有些未能成为詹森多面体的候选多面体是因为其存在有两个以上共面的面,其也可以算是全部由正多边形组成的凸多面体,只是其凸为非严格凸。[2]这些多面体可被看做是凸的面且非常接近正多边形。这些立体通常有无限多种,但若约定所有顶点要位于顶角处,不能位于面(共面的一组面视为同一个面)的内部,则满足条件的立体只有78个,可以视为詹森多面体的自然推广[2](参见条件边正多边形凸多面体)。
例如: 3.3...:
-
同相双三角柱
(菱形柱) -
楔形体
-
二侧锥八面体
(三方偏方面体) -
正三角锥反角柱
-
三侧锥八面体
-
四侧锥八面体
-
四侧锥截角四面体
(截角四面体) -
八侧锥截角八面体
(截角八面体) -
双六角锥柱
(六角柱) -
正三角帐塔锥
(正三角帐塔)
4.4.4.4:
3.4.6.4:
-
正六角帐塔
(退化)
| 部分的条件边正多边形凸多面体 | |
|---|---|
| 侧锥双新月双罩帐 |
二侧锥八面体 |
| 正三角锥反角柱 |
柱化异相双三角柱 |
若将詹森多面体的条件放宽成允许面两两共面,且所有顶点都要严格位于顶角上,不能有边两两共线的情况(若允许边两两共线,则结果会有无穷多种情况),也不能够有顶点位于共面区域内部的情况,则能够再列出有限个有此特性的立体。条件边(conditional edges)指的是对应棱的二面角为平角的边。[2]在这条件下,能允许互相共面的面有正三角形与正三角形(3+3)、正三角形与正方形(3+4)、正三角形与正五边形(3+5)、正方形和两个位于对侧的正三角形(3+4+3)、正五边形和两个不相邻的正三角形(3+5+3),也就是说,这些立体除了有正多边形面外,也会存在上述组合之形状的面。[3]这类立体一共有78个。[2]和詹森多面体一样,这些立体除了一些基本立体外,都能够用柱体、锥体和28种立体互相组合而成。[3]
参见
编辑参考文献
编辑- ^ Kaplan, Craig S.; Hart, George W., Symmetrohedra: Polyhedra from Symmetric Placement of Regular Polygons, Bridges: Mathematical Connections in Art, Music and Science (PDF), 2001 [2014-05-01], (原始内容存档 (PDF)于2015-09-23).
- ^ 2.0 2.1 2.2 2.3 Robert R Tupelo-Schneck. Convex regular-faced polyhedra with conditional edges. [2023-01-31]. (原始内容存档于2021-08-18).
- ^ 3.0 3.1 Robert R Tupelo-Schneck. Regular-faced Polyhedra. [2023-02-01]. (原始内容存档于2022-11-14).