單值性

數學中，單值性（monodromy）研究的是數學分析、代數拓撲、代數幾何與微分幾何中的對象在「繞著奇點旋轉」時的行為。這個領域同覆疊映射及其到分歧的退化密切相關。引發單值現象的方面是，我們想定義一個繞奇點旋轉時不保持單值性的函數。可以定義單值群來測量單值性的失效，這是一群作用於數據的變換，編碼了在單一維度上繞行時發生的情況。單值性的缺乏，有時稱作多值性（polydromy）。^[1]

定義編輯

令X是連通且底局部連通的拓撲空間，基點為x，並令 $p:{\tilde {X}}\to X$ 為覆疊映射，其纖維為 $F=p^{-1}(x)$ 。對以x為基的環圈 $\gamma :\ [0,\ 1]\to X$ ，記從點 ${\tilde {x}}\in F$ 開始的覆疊映射下的提升為 ${\tilde {\gamma }}$ 。最後，用 ${\tilde {x}}\cdot {\tilde {\gamma }}$ 表示端點 ${\tilde {\gamma }}(1)$ ，一半與 ${\tilde {x}}$ 不同。有定理指出，這種構造給出了基本群 $\pi _{1}(X,\ x)$ 在F上的良定義的群作用， ${\tilde {x}}$ 的穩定子恰是 $p_{*}\left(\pi _{1}\left({\tilde {X}},{\tilde {x}}\right)\right)$ ，即若且唯若元素 $[\gamma ]$ 由 ${\tilde {X}}$ 中以 ${\tilde {x}}$ 為基的環圈的像表示時，才會固定F中的一個點。這種作用叫做單值作用，對應的群同態 $\pi _{1}(X,\ x)\to {\rm {Aut}}(H_{*}(F_{x}))$ 映射到F上的自同構群，就是代數單值性。這同態的像就是單值群。還有一個映射 $\pi _{1}(X,\ x)\to {\rm {Diff}}(F_{x})/{\rm {Is}}(F_{x})$ ，其像是拓撲單值群。

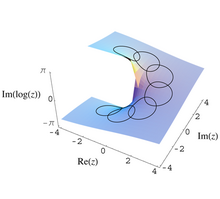
例子編輯

這些觀點首次明確闡述是用複分析的語言。在解析延拓的過程中，在穿孔複平面 $\mathbb {C} \backslash \{0\}$ 的某開子集E中的解析函數 $F(z)$ 可連續映射回E，但值不同。例如，取

{\begin{aligned}F(z)&=\log(z)\\E&=\{z\in \mathbb {C} \mid \operatorname {Re} (z)>0\}\end{aligned}}

然後逆時針繞圓

|z|=1

進行解析延拓，將導致返回的不是 $F(z)$ 而是

F(z)+2\pi i

這時，單值群是無限循環群，覆疊空間是穿孔複平面的萬有覆疊，可以形象理解為螺旋曲面，並有 $\rho >0$ 的約束。覆疊映射是一個垂直投影，從某種意義上說顯然地摺疊了螺旋，得到穿孔平面。

複數域微分方程編輯

一個重要應用是解微分方程，當中單解可通過解析延拓得到更多線性獨立解。複平面中開連通集S上定義的線性微分方程擁有單值群，更精確地說是S基本群的線性表示，概括了S中所有環圈的解析延拓。在給定表示的情況下構造方程（具有正則奇點）的逆問題稱作黎曼–希爾伯特問題。

對於正則（特別是富克斯）線性系統，常常選擇與環圈相應的算子 $M_{j}$ 作為單值群的生成子，當中每個環圈逆時針繞過系統的一個極點。若指標j在順時針繞過極點時從1增加到p+1，則生成子之間的唯一關係是 $M_{1}\cdots M_{p+1}=\operatorname {id}$ 。德利涅–辛普森問題是以下實現問題：對 ${\rm {GL}}(n,\ \mathbb {C} )$ 中的哪些共軛類元組，存在來自這些類的滿足上式的矩陣 $M_{j}$ 的不可約元組？皮埃爾·德利涅與卡洛斯·辛普森第一個得到了問題的解。Vladimir Kostov提出並討論了富克斯系統殘差問題的加性版本。除了 ${\rm {GL}}(n,\ \mathbb {C} )$ 外，其他學者也考慮過在矩陣群上的問題。^[2]

拓撲與幾何角度編輯

在覆疊映射的情形下，我們將其視為纖維化的特例，並利用同倫提升特性「追蹤」基空間X上的路徑（簡單起見假定其是徑連通的），因為它們可提升到覆疊C中。若沿著X中以x為基的環圈繞行，並將其提升到x上方的c處開始，則將在x上方的某個c*處結束。c ≠ c*完全是可能的，為編碼這種情況，可將基本群 $\pi _{1}(X,\ x)$ 的作用視為所有c的集合上的置換群，此時就是單值群。

微分幾何中，平行移動起類似作用。在光滑流形M上的主叢B中，聯絡允許從M上的m之上的纖維「水平」移動到相鄰的纖維。當應用於以m為基的環圈時，其效果是定義了m處纖維平移的完整群；若B的結構群是G，則它就是G的一個子群，衡量了B與積叢 $M\times G$ 的偏差。

單值廣群與葉狀結構編輯

在總空間中有提升基中路徑的路徑。沿著這些路徑推進，就能得到基本廣群的單值作用。

與基本廣群類似，可以繞過基點的選擇，定義單值廣群。此處考慮纖維化 $p:{\tilde {X}}\to X$ 的基空間X中的路徑的提升（的同倫類），結果具有基空間X上的廣群結構。這樣做的好處是，我們可以放棄X的連通性條件。

此外，這個構造還可推廣到葉狀結構：考慮 $(M,{\mathcal {F}})$ 是M的（可能奇異的）葉狀結構。則對於 ${\mathcal {F}}$ 的葉中的每條路徑，都可考慮其在過端點的局部橫截面上的誘導微分同胚。若回到端點周圍的微分同胚的芽，則前述微分同胚在單連通坐標圖中是唯一的，尤其是在不同橫截面之間。這樣，在單連通坐標圖中，它也變得與路徑（固定端點間）無關，因此在同倫下不變。

伽羅瓦理論定義編輯

記 $\mathbb {F} (x)$ 為變量x在F域上的有理函數域，F也是多項式環 $\mathbb {F} [x]$ 的分式域。元素 $f(x)=y\in \mathbb {F} (x)$ 決定了一個有限域擴張 $[\mathbb {F} (x):\ \mathbb {F} (y)]$ 。

這個擴張一般不是伽羅瓦的，但有伽羅瓦閉包 $L(f)$ 。擴張 $[L(f):\ \mathbb {F} (y)]$ 的相關伽羅瓦群稱作f的單值群。

在 $\mathbb {F} =\mathbb {C}$ 的情形下，黎曼曲面理論允許上述幾何解釋。擴張 $[\mathbb {C} (x),\ \mathbb {C} (y)]$ 已經伽羅瓦的情形下，相關單值群有時被稱作甲板變換群（deck transformation）。

這與導致黎曼存在定理的復疊空間伽羅瓦理論有關。

另見編輯

注釋編輯

^ König, Wolfgang; Sprekels, Jürgen. Karl Weierstraß (1815–1897): Aspekte seines Lebens und Werkes – Aspects of his Life and Work. Springer-Verlag. 2015: 200–201 [2017-10-05]. ISBN 9783658106195 （德語）.
^ V. P. Kostov, The Deligne–Simpson problem — a survey, J. Algebra, 2004, 281 (1): 83–108, MR 2091962, S2CID 119634752, arXiv:math/0206298  , doi:10.1016/j.jalgebra.2004.07.013 and the references therein.

參考文獻編輯

V. I. Danilov, Monodromy, Hazewinkel, Michiel (編), 数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4
"Group-groupoids and monodromy groupoids", O. Mucuk, B. Kılıçarslan, T. ¸Sahan, N. Alemdar, Topology and its Applications 158 (2011) 2034–2042 doi:10.1016/j.topol.2011.06.048
R. Brown Topology and Groupoids (2006).
P.J. Higgins, "Categories and groupoids", van Nostrand (1971) TAC Reprint
H. Żołądek, "The Monodromy Group", Birkhäuser Basel 2006; doi: 10.1007/3-7643-7536-1

[König2015-1] König, Wolfgang; Sprekels, Jürgen. Karl Weierstraß (1815–1897): Aspekte seines Lebens und Werkes – Aspects of his Life and Work. Springer-Verlag. 2015: 200–201 [2017-10-05]. ISBN 9783658106195 （德語）.

[2] V. P. Kostov, The Deligne–Simpson problem — a survey, J. Algebra, 2004, 281 (1): 83–108, MR 2091962, S2CID 119634752, arXiv:math/0206298  , doi:10.1016/j.jalgebra.2004.07.013 and the references therein.

[1]

[2]

單值性

定義 編輯

例子 編輯

複數域微分方程 編輯

拓撲與幾何角度 編輯

單值廣群與葉狀結構 編輯

伽羅瓦理論定義 編輯

另見 編輯

注釋 編輯

參考文獻 編輯