在几何学中,六面体是指由六个面组成的多面体。所有面都全等、所有边等长且所有角相等的六面体称为正六面体。几何学上的正六面体是立方体,由6个正方形组成,但在抽象几何学中有另外一种具有6个面的正多面体,是由6个正五边形组成的半十二面体,但其为抽象多胞形不具有体积。其他亦存在所有面都全等但其他条件未必符合正多面体的形状,例如双三角锥和菱形六面体。其他也存在许多不规则的六面体,例如四角锥台、五角锥等。
| 部分的六面体 | |
|---|---|
 三方偏方面体 |
 五角锥 |
 四角柱 |
 双三角锥 |
常见的六面体
编辑常见的六面体有正方体、四角柱、五角锥、双三角锥、三方偏方面体。
长方体
编辑六个面都是矩形的六面体称为长方体,长方体具有每个二面角相等和每个三面角相等等特性。
平行六面体
编辑六个面都是平行四边形的六面体称为平行六面体。当六个面都是菱形时,则具有等边多面体的性质,此时称为菱形六面体。
六面体列表
编辑| 名称 | 图像 | 顶点 | 边 | 面 | 面的种类 | 对称性 | 展开图 |
|---|---|---|---|---|---|---|---|
| 立方体 (正多面体) |
8 | 12 | 6 | 6个正方形 | Oh, [4,3], (*432) order 48 |
||
| 长方体 | 8 | 12 | 6 | 6个矩形 | D2h, [2,2], (*222) order 8 |
||
| 四角柱 (柱体群) |
8 | 12 | 6 | 2个四边形 4个矩形 |
D4h, [4,2], (*422), order 16 | ||
| 五角锥 (锥体群) |
6 | 10 | 6 | 1个五边形 5个三角形 |
C5v, [5], (*55) | ||
| 四角锥台 | 8 | 12 | 6 | 2个四边形 4个梯形 |
C4v, [4], (*44) order 8 | ||
| 菱形六面体 | 8 | 12 | 6 | 6个菱形 | D3d, [2+,6], (2*3) order 12 | ||
| 三方偏方面体 | 8 | 12 | 6 | 6个四边形 | D3, [2,3]+, (223) order 6 | ||
| 双三角锥 | 5 | 9 | 6 | 6个三角形 | D3h, [3,2], (*223) order 12 | ||
| 平行六面体 | 8 | 12 | 6 | 6个平行四边形 | Ci, [2+,2+], (×) order 2 | ||
| 平行六面体 (由菱形组成) |
|||||||
| 十二面体半形 | 10 | 15 | 6 | 6个五边形 | A5, order 60 | ||
| 皮特里正十二面体 | 20 | 30 | 6 | 6个扭歪十边形 | A5×C2, with 120 elements | ||
| 皮特里正二十面体 | 12 | 30 | 6 | 6个扭歪十边形 | |||
| 六面形 | 2 | 6 | 6 | 6个二角形 | D6h(*666) | ||
| 二角反棱柱 | 4 | 8 | 6 | 2个二角形 4个三角形 |
D2d, [2+,4], (2*2), order 8 |
非凸六面体
编辑| 非凸六面体 | ||
|---|---|---|
| 面的种类:4.4.3.3.3.3 10条边、 6个顶点 |
面的种类:5.5.3.3.3.3 11条边、 7个顶点 |
面的种类:6.6.3.3.3.3 12条边、 8个顶点 |
退化六面体
编辑部分六面体包含退化的面或者本身已经退化至无法拥有体积的形式。例如二角反棱柱,其2个底面为二角形,因此退化成一条棱、更进一步的退化六面体有六面形,其由6个二角形组成,本身已退化至无法拥有体积的形式,仅能以球面镶嵌的形式存在。
二角反棱柱
编辑二角反棱柱,又称反二角柱是指底面为二角形的反棱柱,由于其两个底面皆为二角形,因此这两个面已退化成一条棱,若不计这两个退化的底面,则这个立体与四面体无异。在球面几何学中,二角反棱柱可以作为球面镶嵌,此时二角形的面能够在求面上已非退化的形式存在,而确保整个立体为六个面组成的立体,此时的二角反棱柱由2个球面二角形和4个球面三边形构成,共有6个面、8条边和4个顶点,并且可以视为扭棱的二面形或二角形二面体,在施莱夫利符号中可以用sr{2,2}来表示。
 二角反棱柱。上方及下方红色的线段为退化的二角形底面。若不计这两个退化底面,则整个立体与四面体无异 |
 作为球面镶嵌的二角反棱柱。计入二面形面时,二角反棱柱是一种六面体 |
六面形
编辑
六面形是一种多面形,为退化的六面体,无法拥有体积,由六个二角形组成。在球面几何学中,六面形可以在球面上以镶嵌的方式存在,表示六个镶嵌在球体上的球弓形,施莱夫利符号中利用{2,6}来表示,其对偶多面体是六边形二面体。
六面形由六个二角形组成,每个顶点都是六个二角形的公共顶点。正六面形的每个面都是正二角形,且每个顶点都是六个正二角形的公共顶点,因此正六面形也可以视为一种正多面体,但是因为其已退化,因此不会与帕雷托立体一同讨论。
六面形具有D6h, [2,6], (*226)的对称性和D6, [2,6]+的旋转对称性,且阶数为24,在考克斯特符号中用![]()
![]()
![]()
![]()
![]() 表示,其对称性与六角柱相同,因此六角柱也可以视为一种与六面形相关的立体,因为六角柱可以经由六面形透过截角变换构造。
表示,其对称性与六角柱相同,因此六角柱也可以视为一种与六面形相关的立体,因为六角柱可以经由六面形透过截角变换构造。
拓朴学中的六面体
编辑在所有凸六面体当中,共有七种拓朴结构有明显差异的凸六面体[1][2][3][4][5] 。其中有2中互为镜射像。
 双三角锥 36 9 E, 5 V |
 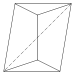 四角反楔体。 有一个手性镜像 面的种类:4.4.3.3.3.3 10条边, 6个顶点 |
 面的种类:4.4.4.4.3.3 11条边, 7个顶点 |
 五角柱 面的种类:5.35 10条边, 6个顶点 |
 面的种类:5.4.4.3.3.3 11条边, 7个顶点 |
 面的种类:5.5.4.4.3.3 12条边, 8个顶点 |
参考文献
编辑- ^ Anatole Beck, Michael Bleicher, Donald Crowe. Excursions into Mathematics: 29–30. 1969.
- ^ Counting polyhedra (页面存档备份,存于互联网档案馆) numericana.com [2016-1-10]
- ^ Martin Gardner. Denkspiele von anderen Planeten. München: Hugendubel. 1986: 134. ISBN 3-88034-295-4.
- ^ Weisstein, Eric W. (编). Hexahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Gardner, M. "Find the Hexahedrons." §19.9 in Martin Gardner's New Mathematical Diversions from Scientific American. New York: Simon and Schuster, pp. 224-225 and 233, 1966.
外部链接
编辑- Polyhedra with 4-7 Faces by Steven Dutch