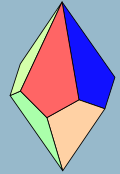
五角反棱柱
由兩個由五個三角形環組成的五邊形組成的反棱柱
(重定向自五角反角柱)
此条目没有列出任何参考或来源。 (2023年10月7日) |
在几何学中,五角反棱柱又称为反五角柱或五角反柱是指底为五边形的反棱柱,侧面由三角形组成,若每一个面皆为正多边形则称为正五角反棱柱。每个五角反棱柱皆含有12个面,是一种十二面体。
 | ||||
| 类别 | 反棱柱 柱状均匀多面体 | |||
|---|---|---|---|---|
| 对偶多面体 | 五方偏方面体 | |||
| 识别 | ||||
| 名称 | 正五角反棱柱 | |||
| 参考索引 | U77(c) | |||
| 鲍尔斯缩写 | pap | |||
| 数学表示法 | ||||
| 考克斯特符号 | ||||
| 施莱夫利符号 | s{2,5} | |||
| 威佐夫符号 | | 2 2 5 | |||
| 康威表示法 | A5 | |||
| 性质 | ||||
| 面 | 12 | |||
| 边 | 20 | |||
| 顶点 | 10 | |||
| 欧拉特征数 | F=12, E=20, V=10 (χ=2) | |||
| 组成与布局 | ||||
| 面的种类 | 三角形×10 正五边形×2 | |||
| 面的布局 | 10{3}+2{5} | |||
| 顶点图 | 3.3.3.5 | |||
| 对称性 | ||||
| 对称群 | D5d, [2+,10], (2*5), order 20 | |||
| 旋转对称群 | D5, [5,2]+, (522), order 10 | |||
| 特性 | ||||
| 凸 | ||||
| 图像 | ||||
| ||||
正五角反棱柱是基底为正五边形的五角反棱柱,其可视为一种半正多面体。
正五角反棱柱也可以视为移除正二十面体底部及顶部的五角锥所构成的立体,因此又称为正二十面体欠对二侧锥。
-
正五角反棱柱
正五角反棱柱
编辑当底面为正五边形时,会具备一些特别的性质
当基底边长为a的时候:
相关多面体与镶嵌
编辑| 对称群:[5,2], (*522) | [5,2]+, (622) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| {5,2} | t{5,2} | r{5,2} | 2t{5,2}=t{2,5} | 2r{5,2}={2,5} | rr{5,2} | tr{5,2} | sr{5,2} | ||
| 半正对偶 | |||||||||
| V52 | V102 | V52 | V4.4.5 | V25 | V4.4.5 | V4.4.10 | V3.3.3.5 | ||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | n |
|---|---|---|---|---|---|---|---|---|---|---|---|
| s{2,4} sr{2,2} |
s{2,6} sr{2,3} |
s{2,8} sr{2,4} |
s{2,10} sr{2,5} |
s{2,12} sr{2,6} |
s{2,14} sr{2,7} |
s{2,16} sr{2,8} |
s{2,18} sr{2,9} |
s{2,20} sr{2,10} |
s{2,22} sr{2,11} |
s{2,24} sr{2,12} |
s{2,2n} sr{2,n} |
| |
|
|
|
|
|
|
|
|
|
|
|
| 作为球面镶嵌 | |||||||||||