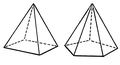
稜錐

角錐
	用線表示的角錐
類別	角錐
對偶多面體	角錐 (本身)
數學表示法
施萊夫利符號	{ } v {n}
性質
面
邊
頂點
歐拉特徵數	F=, E=, V= （χ=2）
組成與佈局
面的種類	n個三角形; 1個正n邊形
對稱性
對稱群	Cnv, [1,n], (*nn), order 2n
旋轉對稱群; （英語：Rotation_groups）	Cn, [1,n+], (nn), order n
特性
	凸
圖像
	; 角錐 (本身); （對偶多面體）
	閱; 論; 編;

在幾何學中，稜錐又稱角錐，是三維多面體的一種，由多邊形各個頂點向它所在的平面外一點依次連直線段而構成。多邊形稱為稜錐的底面。隨著底面形狀不同，稜錐的稱呼也不相同，依底面多邊形而定，例如底面是正方形的稜錐稱為方錐，底面為三角形的稜錐稱為三稜錐，底面為五邊形的稜錐稱為五稜錐等等。

從稜錐的定義可以推知，一個以 $n$ 邊形為底面的稜錐，一共有 $n$ +1個頂點， $n$ +1個面以及2 $n$ 條邊。稜錐的對偶多面體是同樣形狀的稜錐。例如一個方錐的對偶形是（倒立的）方錐。

稜錐的對稱性取決於底面多邊形的形狀和多邊形以外那個頂點的位置。如果底面的多邊形是正多邊形，而且另外一個頂點在底面上的投影是多邊形的中心，那麼稜錐和正多邊形有相同的對稱結構（同構的對稱群）。

稜錐和稜柱、稜台、帳塔一樣，都是擬柱體中的一類。

歷史

在公元前1650年左右的萊因德數學紙草書中，稜錐已經作為數學物件被幾何學家研究。紙草書的56至59題是有關正方錐的底邊、高以及底面和側面形成的二面角之間關係的計算，如已知高和底邊長度，求二面角等^[1]^:30-32。傳說由歐幾里德在公元前三世紀寫成的《幾何原本》中，第十二章第七個命題證明了：三角柱的體積等於同底同高的三角錐的三倍，但《幾何原本》中沒有給出直接的稜錐體積公式^[2]。公元一世紀左右成書的《九章算術》第五章中的第十二題，計算了正方錐、直方錐（陽馬）、直三角錐（鱉臑）的體積，並給出了通用公式。公元三世紀中葉，數學家劉徽在給《九章算術》作的注中，運用極限思想證明了稜錐的體積公式^[3]。

簡介

稜錐的底面是多邊形，其中的頂點和多邊形所在平面外的一點用直線段相連。平面外的這一點稱為稜錐的頂點，底面多邊形的頂點稱為底面頂點。除了底面，其餘的面稱為稜錐的側面，都是由稜錐頂點和多邊形的兩個相鄰頂點構成的三角形。連接底面頂點和稜錐頂點的直線段，也是兩個相鄰側面的公共邊，稱為稜錐的側棱。一個以 $n$ 邊形為底面的稜錐，總計有 $n$ 個側面，加上底面，一共有 $n$ +1個面；多邊形的每個頂點對應一條側棱，一共有 $n$ 條側棱。如果兩條側棱不在同一個側面，那麼它們確定的平面截稜錐所得的截面是一個過稜錐頂點的三角形，其中兩條邊分別是兩條側棱，另一條邊在底面上，是底面多邊形的一條對角線，這個平面稱為稜錐的一個對角面。^[4]^:86

如果底面是三角形，那麼稜錐稱為三稜錐或三角錐。如果每個面（包括底面）都是正三角形，這時的三稜錐就是正四面體。如果僅僅底面為正三角形，頂點在底面的投影是正三角形的中心，那麼三個側面都是全等的等腰三角形。這樣的三稜錐叫做正三稜錐。同樣地，底面為正多邊形，而且另外一個頂點在底面上的投影是多邊形的中心，這樣的稜錐稱為正稜錐。正稜錐的側面都是全等的等腰三角形，側棱都等長。每個側面三角形以多邊形的邊為底邊的話，高稱為稜錐的斜高。^[4]^:86

如果平面外的頂點在底面的投影正好是多邊形的某個頂點（等價於說平面外的頂點和某個頂點連成的直線垂直於底面），這樣的稜錐稱為直稜錐或直角稜錐。連接平面外頂點和其投影頂點的側棱垂直於底面，所以包含這條側棱的兩個側面也垂直於底面。

稜錐的底面多邊形不一定是凸多邊形。如果是星形，則稱為星錐。例如，底面是五角星，則對應的稜錐叫做五星錐。

性質

體積

稜錐的體積取決於平面外頂點到底面的距離，以及底面多邊形的面積。前者稱為稜錐的高，後者稱為稜錐的底面積。設 $h$ 為稜錐的高， $S$ 為稜錐的底面積， $V$ 為稜錐的體積，則稜錐的體積可以用以下公式計算^[4]^:93：

V={\frac {Sh}{3}}

這個公式早在公元三世紀就得到了證明。現代的證明一般使用積分。假設有稜錐 $PA 1 A 2 ...A n$ ，其中 $A 1 A 2 ...A n$ 為底面的 $n$ 邊形， $P$ 為稜錐頂點。設 $P$ 在底面的投影為 $Q$ 點， $PQ$ 的長度為 $h$ 。在線段 $PQ$ 上取一點 $X$ ，使得線段 $PX$ 的長度為 $y$ ：0 $\leq y \leq h$ ，那麼過點 $X$ 而且與底面平行的平面截稜錐得到的形狀是一個和底面的 $n$ 邊形相似的 $n$ 邊形，記作 $A x1 A x2 ...A xn$ ，它的面積 $S y$ 與底面積 $S$ 的比值等於 $PX$ 與 $PQ$ 的比值的平方：

{\frac {S_{y}}{S}}=\left({\frac {PX}{PQ}}\right)^{2}=\left({\frac {y}{h}}\right)^{2}.

在點 $X$ 附近截取的「一片」稜錐「切片」，它的體積大約等於： $dV_{y}\approx \left({\frac {y}{h}}\right)^{2}Sdy$

所以稜錐的體積等於積分： $V=\int _{y=0}^{h}dV_{y}=\int _{y=0}^{h}\left({\frac {y}{h}}\right)^{2}Sdy={\frac {h^{3}}{3}}\cdot {\frac {S}{h^{2}}}={\frac {1}{3}}Sh.$

對於正稜錐，假設它的底面是正 $n$ 邊形，邊長為 $a$ ，高是 $h$ ，那麼底面積是： $S={\frac {na^{2}}{4}}\cot {\frac {\pi }{n}}.$ 所以它的體積是：

V={\frac {na^{2}h}{12}}\cot {\frac {\pi }{n}}.

表面積

稜錐的側面展開圖是由各個側面組成的，展開圖的面積，就是稜錐的側面積 $S c$

S_{c}=\sum _{i=1}^{n}S_{i}

，其中

S_{i},i=1,2\cdots ,n

是第 i 個側面的面積。

稜錐的表面積等於稜錐的側面積 $S c$ 加上底面積 $S$ 。假設頂點的投影 $Q$ 點到第 i 個側面對應的底邊的距離是 $d i$ ，底邊的長度是 $a i$ ，那麼稜錐的側面積：

S_{c}=\sum _{i=1}^{n}S_{i}={\frac {1}{2}}\sum _{i=1}^{n}a_{i}{\sqrt {h^{2}+d_{i}^{2}}}.

對於正 $n$ 稜錐，頂點到底面的投影是底面正 $n$ 邊形的中心。所以投影點到每一邊的距離都相等： $d_{1}=d_{2}=\cdots =d_{n}=d.$ 因此稜錐的斜高也就是側面三角形的高： $l={\sqrt {h^{2}+d^{2}}}.$ 稜錐的側面積^[4]^:87：

S_{c}=\sum _{i=1}^{n}S_{i}={\frac {1}{2}}l\sum _{i=1}^{n}a_{i}={\frac {1}{2}}lp.

其中 $p$ 是底面正 $n$ 邊形的周長。假設底面正 $n$ 邊形的邊長是 $a$ ，高是 $h$ ，那麼它的周長是 $na$ ，中心到每一邊的距離是 ${\frac {a}{2}}\cot {\frac {\pi }{n}}$ 。所以斜高是： ${\sqrt {h^{2}+{\frac {a^{2}}{4}}\cot ^{2}{\frac {\pi }{n}}}}$ ，側面積是：

S_{c}=\sum _{i=1}^{n}S_{i}={\frac {1}{2}}na{\sqrt {h^{2}+{\frac {a^{2}}{4}}\cot ^{2}{\frac {\pi }{n}}}}.

正稜錐

若一錐體底面為正多邊形則稱為正稜錐。正稜錐是一個無窮集合，最小從三角錐開始，因為二角錐已退化成平面了。

稜錐體
正二棱錐	正三棱錐	正四棱錐	正五棱錐	正六棱錐	正七棱錐	正八棱錐	正九棱錐	正十棱錐	...	圓錐

此外錐體亦可以做為球面鑲嵌：

錐體形式鑲嵌系列：
球面鑲嵌		錐體									歐式鑲嵌仿緊空間	雙曲鑲嵌非緊空間
一角錐 C_1v, [1]	二角錐 C_2v, [2]	三角錐 C_3v, [3]	四角錐 C_4v, [4]	五角錐 C_5v, [5]	六角錐 C_6v, [6]	七角錐 C_7v, [7]	八角錐 C_8v, [8]	九角錐 C_9v, [9]	十角錐 C_10v, [10]	...	無限角錐 C_∞v, [∞]	超無限角錐 C_iπ/λv, [iπ/λ]

錐體中只有一種屬於正多面體，即正三角錐。

參看

金字塔：某些金字塔是稜錐狀建築，大部分是四稜錐；
圓錐：底面為圓形而不是多邊形的錐體；
稜台：將稜柱沿平行於底面的平面截取出來的幾何體。
雙錐體：將稜錐於底面相接合所形成的幾何體。
類錐體：稜柱與反稜柱之關係在稜錐上的類比

參考來源

^ Roger Herz-Fischler. The Shape of the Great Pyramid. Wilfrid Laurier Univ. Press（插圖版）. 2000. ISBN 9780889203242.
^ The Elements of Euclid, Book XII.5-7.
^ 《九章算術》，劉徽注，第五章
^ ^4.0 ^4.1 ^4.2 ^4.3 H. E. Slaught, N. J. Lennes. Solid Geometry, with Problems and Applications (PDF). Allyn and Bacon. 1919 [2013-09-22]. ISBN 1103016261. （原始內容存檔 (PDF)於2019-09-27）（英語）.

外部連結

埃里克·韋斯坦因. Pyramid. MathWorld.
Olshevsky, George, Pyramid at Glossary for Hyperspace.
The Uniform Polyhedra （頁面存檔備份，存於網際網路檔案館）

[rhf-3] Roger Herz-Fischler. The Shape of the Great Pyramid. Wilfrid Laurier Univ. Press（插圖版）. 2000. ISBN 9780889203242.

[euclid-4] The Elements of Euclid, Book XII.5-7.

[jzss-5] 《九章算術》，劉徽注，第五章

[sl-6] 4.0 ^4.1 ^4.2 ^4.3 H. E. Slaught, N. J. Lennes. Solid Geometry, with Problems and Applications (PDF). Allyn and Bacon. 1919 [2013-09-22]. ISBN 1103016261. （原始內容存檔 (PDF)於2019-09-27）（英語）.

[1]

[2]

[3]

[4]